What are Numbers? Or, Learning to Count!
Posted 17th April 2021 by Holger
We all use numbers every day and some of us feel more comfortable dealing with them than others. But have you ever asked yourself what numbers really are? For example, what is the number 4? Of course, you can describe the symbol “4”. But that is not really the number, is it? You can use Roman numerals IV, Urdu ۴, or Chinese and Japanese Kanji 四. Each one of these symbols represents the same number. And yet, somehow we would all probably agree that there is only one number 4.
The question about the nature of numbers is twofold. You can understand this question purely mathematical one and ask for a clear definition of a number and the set of numbers in a mathematical sense. This will be the topic of this article. You can also ask yourself what numbers are in a philosophical sense. Do numbers exist? If yes, in what way do they exist, and what are they? This may be the topic of a future article.
Now that we have settled what type of question we want to answer, we should start with the simplest type of numbers. These are the natural numbers 0, 1, 2, 3, 4, …
I decided to include the number zero even though it might seem a little abstract at first. After all, what does it mean to have zero of something? But that objection strays into the philosophical realm again and, as I said above, I want to focus on the mathematical aspect here.
When doing the research for this article, I was slightly surprised at the plethora of different definitions for the natural numbers. But given how fundamental this question is, it should be no wonder that many mathematicians have thought about the problem of defining numbers and have come up with different answers.
The Peano Axioms
Let’s start with an axiomatic definition of numbers called the Peano axioms. This is one of the earliest strict definitions of the natural numbers in the modern sense. It doesn’t really state what the natural numbers are but focuses on how they behave. We start with the set of natural numbers, which we call $\mathbb{N}$, and a successor function $S$.
Peano Axiom 1:
$0$ is a natural number or, more formally, $0 \in \mathbb{N}$
This axiom just tells us that there is a natural number zero. We could have chosen 1 as the starting point but this is arbitrary.
Peano Axiom 2:
Every natural number $x$ has a successor $y$.
In other words, given that $x \in \mathbb{N}$ then it follows that $y = S(x) \in \mathbb{N}$.
Intuitively, the successor function will always produce the next natural number.
Mathematicians call this property of the natural number being closed under the successor operation $S$. All this means is that the successor operation will never produce a result that is outside of the natural numbers.
Peano Axiom 3:
If we have two natural numbers $x$ and $y$, and we know that the successors of $x$ and $y$ are equal, then this is the same as saying that $x$ and $y$ are equal.
Again, written more formally we say, given $x \in \mathbb{N}$ and $y \in \mathbb{N}$ and $S(x) = S(y)$ then it follows that $x=y$.
This means that any natural number cannot be the successor of two different number. In other words, if you have two different numbers then they can’t have the same successor.
Peano Axiom 4:
$0$ is not the successor of any other natural number.
In mathematical notation, if $x \in \mathbb{N}$ then $S(x) \ne 0$
At first sight, we might think that these axioms are complete. We can start from zero and use the successor function $S$ to iterate through the natural numbers. This is intuitively shown in the image below.
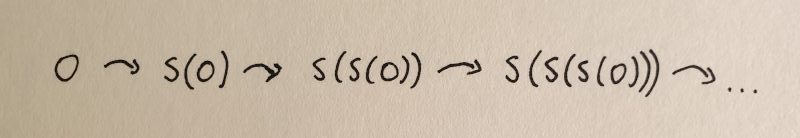
Repeatedly applying the successor function, starting from 0.
Here
1 = S(0)
2 = S(S(0)) = S(1)
3 = S(S(S(0))) = S(2)
and so on.
But we haven’t guaranteed that this iteration will eventually be able to reach all natural numbers. Imagine that, in addition to the above, there is some special number $z$ that creates a closed loop when applying the successor function. And this loop is separate from the sequence that we get when starting from zero.

A closed loop of successors that isn’t connected to the zero element.
So we need another axiom that guarantees that all natural numbers are reachable from zero by repeatedly applying the successor function. This axiom is usually stated in the following way.
Peano Axiom 5: Axiom of Induction
Given any set $U \subseteq \mathbb{N}$ with $0 \in U$.
If $U$ is such that for every $n \in U$ the successor is also in $U$, i.e. $S(n) \in U$,
then $U = \mathbb{N}$
The idea behind this axiom is that $U$ can be chosen as the minimal set that contains no additional loops or numbers that are not reachable from zero. The fact that any set $U$ that contains zero and is closed under the successor function is identical to the natural numbers guarantees that all natural numbers are eventually reachable from zero. The axiom of induction is maybe more familiar in its alternative form.
Peano Axiom 5: Axiom of Induction, alternative form
Consider a mathematical statement that is true for zero.
If it can be proven that,
given the statement is true for a number $n$, then it is also true for $S(n)$,
then it follows that the statement is true for all natural numbers.
Here you can see that this axiom forms the basis of the familiar proof by induction.
Some Remarks
The Peano Axioms are helpful in defining the set of natural numbers $\mathbb{N}$ and arithmetic operations on them. But personally, I feel unsatisfied by this definition. The Peano Axioms tell us how natural numbers behave but they don’t really give any additional insight as to what numbers really are.
Take for example the number 2. We now know that 2 can be expressed as the successor of the successor of 0, i.e. $2 = S(S(0))$. We also know that this second successor must be a member of the set of natural numbers, but not much more. The problem here is that we never defined what the successor function should be.
Nonetheless, the Peano axioms can serve as a basis for more in-depth definitions of the natural numbers. These definitions can be considered models of the Peano Axioms in the sense that they define a zero element and some concrete successor function. The set of natural numbers can then be constructed from these and the Peano Axioms follow as consequences from these definitions.
In a future post, I will look at some set-theoretic definitions of the natural numbers. If you liked this post, please leave a comment and check back soon for more content.
Leave a Reply