Computational Physics Basics: Floating Point Numbers

Posted 25th May 2021 by Holger Schmitz

In a previous contribution, I have shown you that computers are naturally suited to store finite length integer numbers. Most quantities in physics, on the other hand, are real numbers. Computers can store real numbers only with finite precision. Like storing integers, each representation of a real number is stored in a finite number of bits. Two aspects need to be considered. The precision of the stored number is the number of significant decimal places that can be represented. Higher precision means that the error of the representation can be made smaller. Bur precision is not the only aspect that needs consideration. Often, physical quantities can be very large or very small. The electron charge in SI units, for example, is roughly $1.602\times10^{-19}$C. Using a fixed point decimal format to represent this number would require a large number of unnecessary zeros to be stored. Therefore, the range of numbers that can be represented is also important.

In the decimal system, we already have a notation that can capture very large and very small numbers and I have used it to write down the electron charge in the example above. The scientific notation writes a number as a product of a mantissa and a power of 10. The value of the electron charge (without units) is written as
$$1.602\times10^{-19}.$$
Here 1.602 is the mantissa (or the significand) and -19 is the exponent. The general form is
$$m\times 10^n.$$
The mantissa, $m$, will always be between 1 and 10 and the exponent, $n$, has to be chosen accordingly. This format can straight away be translated into the binary system. Here, any number can be written as
$$m\times2^n,$$
with $1\le m<2$. Both $m$ and $n$ can be stored in binary form.

Memory layout of floating-point numbers, the IEEE 754 standard

In most modern computers, numbers are stored using 64 bits but some architectures, like smartphones, might only use 32 bits. For a given number of bits, a decision has to be made on how many bits should be used to store the mantissa and how many bits should be used for the exponent. The IEEE 754 standard sets out the memory layout for various size floating-point representations and almost all hardware supports these specifications. The following table shows the number of bits for mantissa and exponent for some IEEE 754 number formats.

Bits	Name	Sign bit	Mantissa bits, m	Exponent bits, p	Exponent bias	Decimal digits
16	half-precision	1	10	5	15	3.31
32	single precision	1	23	8	127	7.22
64	double precision	1	52	11	1023	15.95
128	quadruple precision	1	112	15	16383	34.02

The layout of the bits is as follows. The first, most significant bit represents the sign of the number. A 0 indicates a positive number and a 1 indicates a negative number. The next $p$ bits store the exponent. The exponent is not stored as a signed integer, but as an unsigned integer with offset. This offset, or bias, is chosen to be $2^p – 1$ so that a leading zero followed by all ones corresponds to an exponent of 0.

The remaining bits store the mantissa. The mantissa is always between 1 and less than 2. This means that, in binary, the leading bit is always equal to one and doesn’t need to be stored. The $m$ bits, therefore, only store the fractional part of the mantissa. This allows for one extra bit to improve the precision of the number.

Example

Infinity and NaN

The IEEE 754 standard defines special numbers that represent infinity and the not-a-number state. Infinity is used to show that a result of a computation has exceeded the allowed range. It can also result from a division by zero. Infinity is represented by the maximum exponent, i.e. all $p$ bits of the exponent are set to 1. In addition, the $m$ bits of the mantissa are set to 0. The sign bit is still used for infinity. This means it is possible to store a +Inf and a -Inf value.

Example

The special state NaN is used to store results that are not defined or can’t otherwise be represented. For example, the operation $\sqrt{-1}$ will result in a not-a-number state. Similar to infinity, it is represented by setting the $p$ exponent bits to 1. To distinguish it from infinity, the mantissa can have any non-zero value.

Subnormal Numbers

As stated above, all numbers in the regular range will be represented by a mantissa between 1 and 2 so that the leading bit is always 1. Numbers very close to zero will have a small exponent value. Once the exponent is exactly zero, it is better to explicitly store all bits of the mantissa and allow the first bit to be zero. This allows even smaller numbers to be represented than would otherwise be possible. Extending the range in this way comes at the cost of reduced precision of the stored number.

Example

Floating Point Numbers in Python, C++, and JavaScript

Both Python and JavaScript exclusively store floating-point numbers using 64-bit precision. In fact, in JavaScript, all numbers are stored as 64-bit floating-point, even integers. This is the reason for the fact that integers in JavaScript only have 53 bits. They are stored in the mantissa of the 64-bit floating-point number.

C++ offers a choice of different precisions

Type	Alternative Name	Number of Bits
float	single precision	usually 32 bits
double	double precision	usually 64 bits
long double	extended precision	architecture-dependent, not IEEE 754, usually 80 bits

Read More

Computational Physics Basics: How Integers are Stored

Posted 4th April 2020 by Holger Schmitz

Unsigned Integers

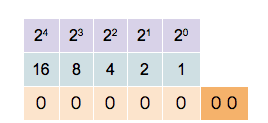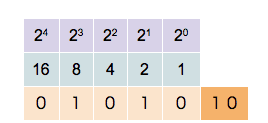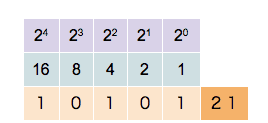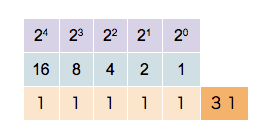
Computers use binary representations to store various types of data. In the context of computational physics, it is important to understand how numerical values are stored. To start, let’s take a look at non-negative integer numbers. These unsigned integers can simply be translated into their binary representation. The binary number-format is similar to the all-familiar decimal format with the main difference that there are only two values for the digits, not ten. The two values are 0 and 1. Numbers are written in the same way as decimal numbers only that the place values of each digit are now powers of 2. For example, the following 4-digit numbers show the values of the first four

0 0 0 1   decimal value 2⁰ = 1
0 0 1 0   decimal value 2¹ = 2
0 1 0 0   decimal value 2² = 4
1 0 0 0   decimal value 2³ = 8

The binary digits are called bits and in modern computers, the bits are grouped in units of 8. Each unit of 8 bits is called a byte and can contain values between 0 and 2⁸ − 1 = 255. Of course, 255 is not a very large number and for most applications, larger numbers are needed. Most modern computer architectures support integers with 32 bits and 64 bits. Unsigned 32-bit integers range from 0 to 2³² − 1 = 4, 294, 967, 295 ≈ 4.3 × 10⁹ and unsigned 64-bit integers range from 0 to 2⁶⁴ − 1 = 18, 446, 744, 073, 709, 551, 615 ≈ 1.8 × 10¹⁹. It is worthwhile noting that many GPU architectures currently don’t natively support 64-bit numbers.

The computer’s processor contains registers that can store binary numbers. Thus a 64-bit processor contains 64-bit registers and has machine instructions that perform numerical operations on those registers. As an example, consider the addition operation. In binary, two numbers are added in much the same way as using long addition in decimal. Consider the addition of two 64 bit integers 7013356221863432502 + 884350303838366524. In binary, this is written as follows.

  01100001,01010100,01110010,01010011,01001111,01110010,00010001,00110110
+ 00001100,01000101,11010111,11101010,01110101,01001011,01101011,00111100
---------------------------------------------------------------------------
  01101101,10011010,01001010,00111101,11000100,10111101,01111100,01110010

The process of adding two numbers is simple. From right to left, the digits of the two numbers are added. If the result is two or more, there will be a carry-over which is added to the next digit on the left.

You could add integers of any size using this prescription but, of course, in the computer numbers are limited by the number of bits they contain. Consider the following binary addition of (2⁶⁴ − 1) and 1 .

  11111111,11111111,11111111,11111111,11111111,11111111,11111111,11111111
+ 00000000,00000000,00000000,00000000,00000000,00000000,00000000,00000001
---------------------------------------------------------------------------
  00000000,00000000,00000000,00000000,00000000,00000000,00000000,00000000

If you were dealing with mathematical integers, you would expect to see an extra digit 1 on the left. The computer cannot store that bit in the register containing the result but stores the extra bit in a special carry flag. In many computer languages, this unintentional overflow will go undetected and the programmer has to take care that numerical operations do not lead to unintended results.

Signed Integers

The example above shows that adding two non-zero numbers can result in 0. This can be exploited to define negative numbers. In general, given a number a, the negative  − a is defined as the number that solves the equation
a + ( − a) = 0.
Mathematically, the N-bit integers can be seen as the group of integers modulo 2^N. This means that for any number a ∈ {0, …, 2^N − 1} the number  − a can be defined as
 − a = 2^N − a ∈ {0, …, 2^N − 1}.
By convention, all numbers whose highest value binary bit is zero are considered positive. Those numbers whose highest value bit is one are considered negative. This makes the addition and subtraction of signed integers straightforward as the processor does not need to implement different algorithms for positive or negative numbers. Signed 32-bit integers range from  − 2, 147, 483, 648 to 2, 147, 483, 647, and 64-bit integers range from  − 9, 223, 372, 036, 854, 775, 808 to 9, 223, 372, 036, 854, 775, 807.

This format of storing negative numbers is called the two’s complement format. The reason for this name becomes obvious when observing how to transform a positive number to its negative.

01100001,01010100,01110010,01010011,01001111,01110010,00010001,00110110 (7013356221863432502)
10011110,10101011,10001101,10101100,10110000,10001101,11101110,11001010 (-7013356221863432502)

To invert a number, first, invert all its bits and then add 1. This simple rule of taking the two’s complement can be easily implemented in the processor’s hardware. Because of the simplicity of this prescription, and the fact that adding a negative number follows the same algorithm as adding a positive number, two’s complement is de-facto the only format used to store negative integers on modern processors.

Exercises

1. Show that taking the two’s complement of an N-bit number a does indeed result in the negative  − a if the addition of two numbers is defined as the addition modulo 2^N.
2. Find out how integers are represented in the programming language of your choice. Does this directly reflect the representation of the underlying architecture? I will be writing another post about this topic soon.
3. Most processors have native commands for multiplying two integers. The result of multiplying the numbers in two N-bit registers are stored in two N-bit result registers representing the high and low bits of the result. Show that the resulting 2N bits will always be enough to store the result.
4. Show how the multiplication of two numbers can be implemented using only the bit-shift operator and conditional addition based on the bit that has been shifted out of the register. The bit-shift operator simply shifts all bits of a register to the left or right.

Read More