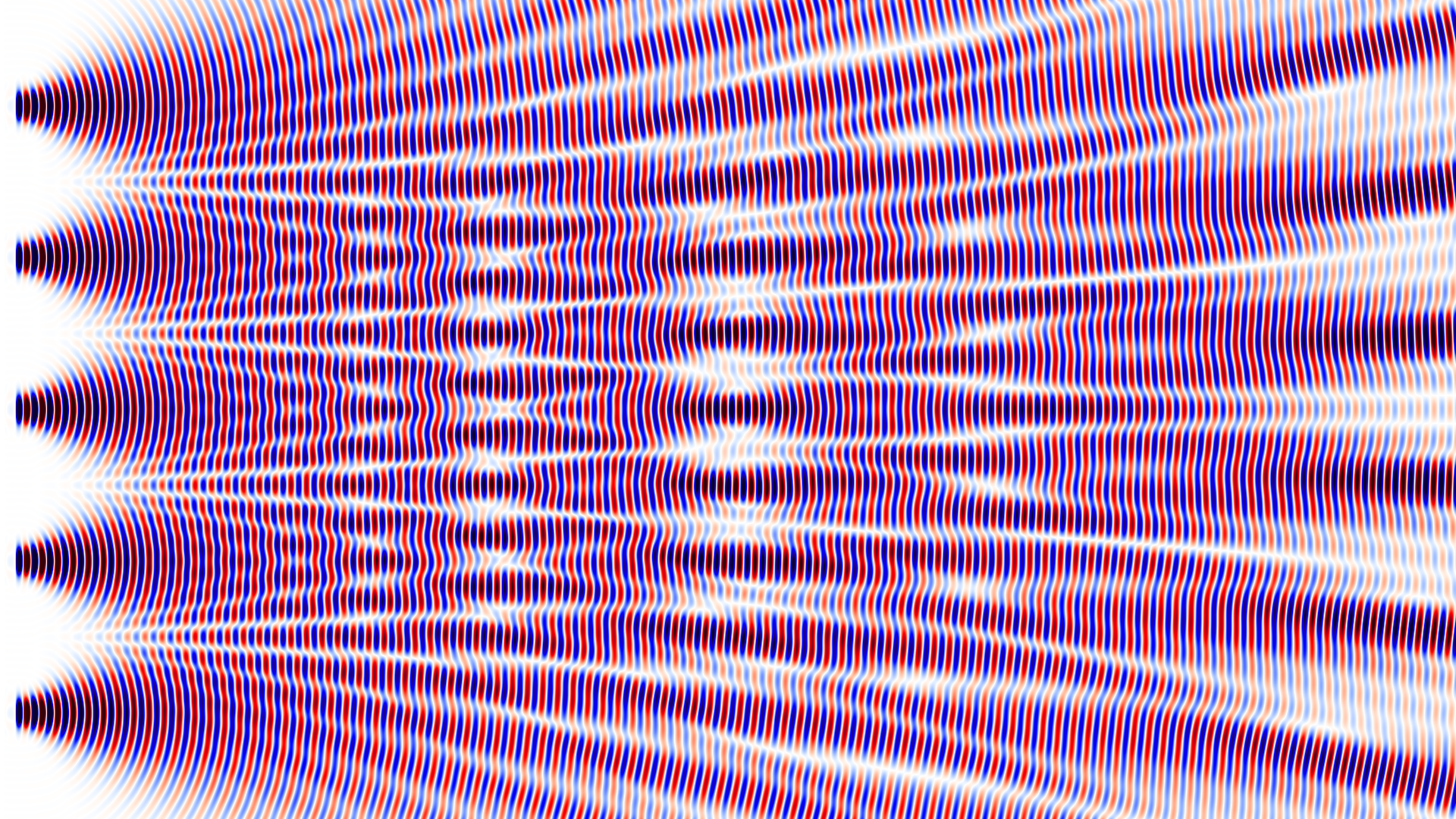
Multi Slit Interference
Posted 11th September 2021 by Holger Schmitz
This week I have been playing around with my electromagnetic wave simulation code MPulse. The code simulates Maxwell’s equations using an algorithm known as finite-difference time-domain, FDTD for short. Here, I am simulating the wave interference pattern behind the screen with n slits. For $n=1$ there is only one slit and no interference at all. The slit is less than the wavelength wide so you can see the wave spreading out at a large angle. When $n>1$ the slits are 5 wavelengths apart. With $n=2$ you have the classical double-slit experiment. At the right side of the simulation box, the well-known interference pattern can be observed. For 3 slits the pattern close to the slits becomes more complicated. It settles down to a stable pattern much further to the right. For numbers 4, 5 and 6 the patterns become more and more interesting. You would expect the development of sharper lines but it turns out that, for these larger numbers, the simulation box just wasn’t big enough to see the final far-field pattern.
MPulse is open-source and is available at https://github.com/holgerschmitz/MPulse.
The code uses MPI parallelization and was run on 24 cores for this simulation.
MPulse is a work in progress and any help from enthusiastic developers is greatly appreciated.
Spherical Blast Wave Simulation
Posted 2nd December 2020 by Holger Schmitz
Here is another animation that I made using the Vellamo fluid code. It shows two very simple simulations of spherical blast waves. The first simulation has been carried out in two dimensions. The second one shows a very similar setup but in three dimensions.
You might have seen some youtube videos on blast waves and dimensional analysis on the Sixty Symbols channel or on Numberphile. The criterion for the dimensional analysis given in those videos is true for strong blast waves. The simulation that I carried out, looks at the later stage of these waves when the energy peters out and the strong shock is replaced by a compression wave that travels at a constant velocity. You can still see some of the self-similar behaviour of the Sedov-Taylor solution during the very early stages of the explosion. But after the speed of the shock has slowed down to the sound speed, the compression wave continues to travel at the speed of sound, gradually losing its energy.
The video shows the energy density over time. The energy density includes the thermal energy as well as the kinetic energy of the gas.
For those of you who are interested in the maths and the physics, the code simulates the Euler equations of a compressible fluid. These equations are a model for an ideal adiabatic gas. For more information about the Euler equations check out my previous post.