Fifty Solitaires – Laying it Out
Posted 3rd May 2024 by Holger Schmitz
The last time I wrote about my Fifty Solitaires project, I focused on updating all my package dependencies and making sure that my components still worked when using newer versions of React and Storybook. This time, I will make some progress by creating the Tableau component. In Solitaire, the Tableau is the area where the cards are laid out. Each pile of cards has a specified location and rules on which cards are visible and how cards can be taken or dropped onto the pile. For the scope of this post, I will keep the Tableau component relatively simple. In previous posts, I already created the Card and Pile components. For now, the Tableau will simply consist of a set of Piles laid out on a rectangular grid. The rules for moving and uncovering cards will be implemented in a later post.
The Grid
In the first step, I think about the information I will need to display the Tableau. I can already display piles of cards using the Pile component and the properties passed into the Pile component is defined by PileProperties. To display a pile on the Tableau, I will also need the location of the Pile. The natural way of determining the position, is to think of the Tableau as a rectangular grid with rows and columns. Each Pile will have a row and column number. This leads me to define PileDisplayProperties in the following way.
import { PileProperties } from "./Pile";
export interface PileDisplayProperties extends PileProperties {
row: number;
col: number;
}I am adding this code to a new file in src/components/Tableau.tsx. The TableauProperties will be the datatype passed into the Tableau component. This consists of an array of piles specified by PileDisplayProperties and a total number of rows and columns of the grid.
export interface TableauProperties {
rows: number;
cols: number;
piles: PileDisplayProperties[];
}The natural way to lay out the Tableau component in CSS is by using the display: grid property. This is a relatively new layout concept in CSS but it has been around for a while and is supported by all modern browsers. I’ll jump ahead a bit and first show you the CSS for the Tableau so that the implementation of the component makes sense. In a new file, src/components/Tableau.css, I placed the following code.
.solitaire-tableau {
display: grid;
background-color: #009900;
position: relative;
}This simply sets the display property to grid and also sets a nice green background color, representative of the green felt usually found on card game tables. If you are unfamiliar with the grid layouts in CSS, I find the Complete Guide to CSS Grid on CSS-Tricks a very useful starting point. You will notice that a grid usually needs column and row definitions. These are missing from my CSS file because they depend on the rows and cols parameters passed into the component.
The Tableau Component
Using this CSS, and the type definitions above, I can now create the Tableau component in src/components/Tableau.tsx.
import './Tableau.css';
export function Tableau({rows, cols, piles}: TableauProperties) {
// some code to check the component width and set the `width` variable
const gutter = 0.1*width/cols;
const cellWidth = width/cols - gutter;
const cellHeight = 1.45*cellWidth - gutter;
const tableauStyle: CSSProperties = {
gridTemplateColumns: `repeat(${cols}, ${cellWidth}px)`,
gridTemplateRows: `repeat(${rows}, ${cellHeight}px)`,
rowGap: `${gutter}px`,
columnGap: `${gutter}px`
};
return (<div ref={ref} className="solitaire-tableau" style={tableauStyle}>
{piles.map((pile, index) => {
const pileStyle: CSSProperties = {
gridRow: `${pile.row} / span 1`,
gridColumn: `${pile.col} / span 1`,
left: '0px'
};
return <div className="pile-container" style={pileStyle}>
<Pile
pile={pile.pile}
direction={pile.direction}
key={index}
/>
</div>
})}
</div>)
}In this component, all measures are calculated as fractions of the grid’s width, given in the width variable. You will note that I haven’t implemented how I obtain the value of this width yet. I will do that below. Each cell in the grid will have a total cell width, including gutters, of width/cols. The gutter is set 10% of this space and the remaining width for the cell is stored in cellWidth. Because the aspect ratio of the cards is constant, the cellHeight is given by the 1.45 times the cell with, subtracting the gutter again. The tableauStyle variable then contains all the CSS that is calculated dynamically based on the window width and number of columns in the grid.
The actual component is a div with class solitaire-tableau so that the CSS from the stylesheet is applied. The dynamic styles are passed in via the style attribute. The solitaire-tableau div is now styled a a CSS grid where the rows and columns are given by the parameters passed to the Tableau component. The next step is to populate those cells that contain card piles. This is done by iterating over the piles array and creating divs containing Pile components. Each of these divs gets some element CSS defining the gridRow and gridColumn CSS properties. This places each pile at the location in the grid that is defined by pile.row and pile.col.
Dynamic Width Calculation
All that’s left to do is to make sure that the width variable is set to correct width of the Tableau component. This width might change if the window resizes, so I will have to dynamically update this width. You will see that I have attached a ref attribute to the solitaire-tableau div. I now add the following code at the top inside the Tableau component, replacing the comment about the width variable.
const ref = useRef<HTMLDivElement>(null);
const [width, setWidth] = useState(0);
function autoResize() {
const widthTot = ref.current?.parentElement?.offsetWidth ?? 0;
const widthLoc = Math.min(widthTot, 1024);
setWidth(widthLoc);
}
useLayoutEffect(() => {
window.addEventListener('resize', autoResize);
autoResize();
return () => {
window.removeEventListener('resize', autoResize);
};
}, []);width is a state variable that gets updated every time the layout changes. It is initialised using the useState hook and then set in the autoResize function. I use the ref to obtain the parent element’s width. This is given by the offsetWidth property on the element. I then limit the width of the tableau to 1024px before updating the width state with setWidth. The useLayoutEffect hook is then used to call the autoResize function. By adding the function as an an event listener to the resize event, I ensure that the width is updated every time the window size changes. Note that the return value of useLayoutEffect is a function that is used for cleanup. To avoid memory leaks, I make sure that the event listener is remove during cleanup of the Tableau component.
To make all of this work, I also need to update the imports at the top of the file. The imports in Tableau.tsx now look like this.
import { CSSProperties, useLayoutEffect, useRef, useState } from "react";
import { Pile, PileProperties } from "./Pile";
import './Tableau.css';Viewing the Tableau in Storybook
To view the Tableau component in Storybook, I created a file src/stories/Tableau.stories.tsx. For completeness, I will paste the content of the file here although it is not very enlightening. All it does is create a few piles with cards in them and adds these piles to the TableauProperties for display. Here is the file.
import { Tableau, TableauProperties, PileDisplayProperties } from '../components/Tableau';
import { Direction } from '../components/Pile';
import { CardSuit, CardValue } from '../components/Card';
export default {
component: Tableau,
title: 'Components/Tableau',
};
interface StoryTableauProperties extends TableauProperties {
style: { [key: string]: string}
}
const pileOpen: PileDisplayProperties = {
pile: [
{ suit: CardSuit.clubs, value: CardValue.ace, faceUp: true, open: true },
{ suit: CardSuit.clubs, value: CardValue.three, faceUp: true, open: true },
{ suit: CardSuit.diamonds, value: CardValue.eight, faceUp: true, open: true },
],
direction: Direction.south,
row: 1,
col: 1
}
const pileClosed: PileDisplayProperties = {
pile: [
{ suit: CardSuit.clubs, value: CardValue.ace, faceUp: true, open: false },
{ suit: CardSuit.clubs, value: CardValue.three, faceUp: true, open: false },
{ suit: CardSuit.diamonds, value: CardValue.eight, faceUp: true, open: false },
],
direction: Direction.south,
row: 1,
col: 2
}
const pileMixed: PileDisplayProperties = {
pile: [
{ suit: CardSuit.clubs, value: CardValue.ace, faceUp: true, open: false },
{ suit: CardSuit.clubs, value: CardValue.three, faceUp: true, open: false },
{ suit: CardSuit.diamonds, value: CardValue.eight, faceUp: true, open: false },
{ suit: CardSuit.hearts, value: CardValue.jack, faceUp: true, open: true },
{ suit: CardSuit.spades, value: CardValue.four, faceUp: true, open: true },
{ suit: CardSuit.hearts, value: CardValue.seven, faceUp: true, open: true },
],
direction: Direction.east,
row: 3,
col: 1
}
const pileFaceUpAndDown: PileDisplayProperties = {
pile: [
{ suit: CardSuit.clubs, value: CardValue.ace, faceUp: false, open: true },
{ suit: CardSuit.clubs, value: CardValue.three, faceUp: false, open: true },
{ suit: CardSuit.spades, value: CardValue.four, faceUp: true, open: true },
{ suit: CardSuit.hearts, value: CardValue.seven, faceUp: true, open: true },
],
direction: Direction.west,
row: 1,
col: 8
};
function Template(args: StoryTableauProperties) {
return <div style={({
display: 'flex',
justifyContent: "center",
width: "100%",
})}>
<div style={args.style}><Tableau {...args} /></div>
</div>
};
export const SolitaireTableau = Template.bind({});
(SolitaireTableau as any).args = {
piles: [
pileClosed,
pileOpen,
pileMixed,
pileFaceUpAndDown
],
rows: 5,
cols: 8,
style: {
width: '100%',
backgroundColor: '#444444',
padding: 10
}
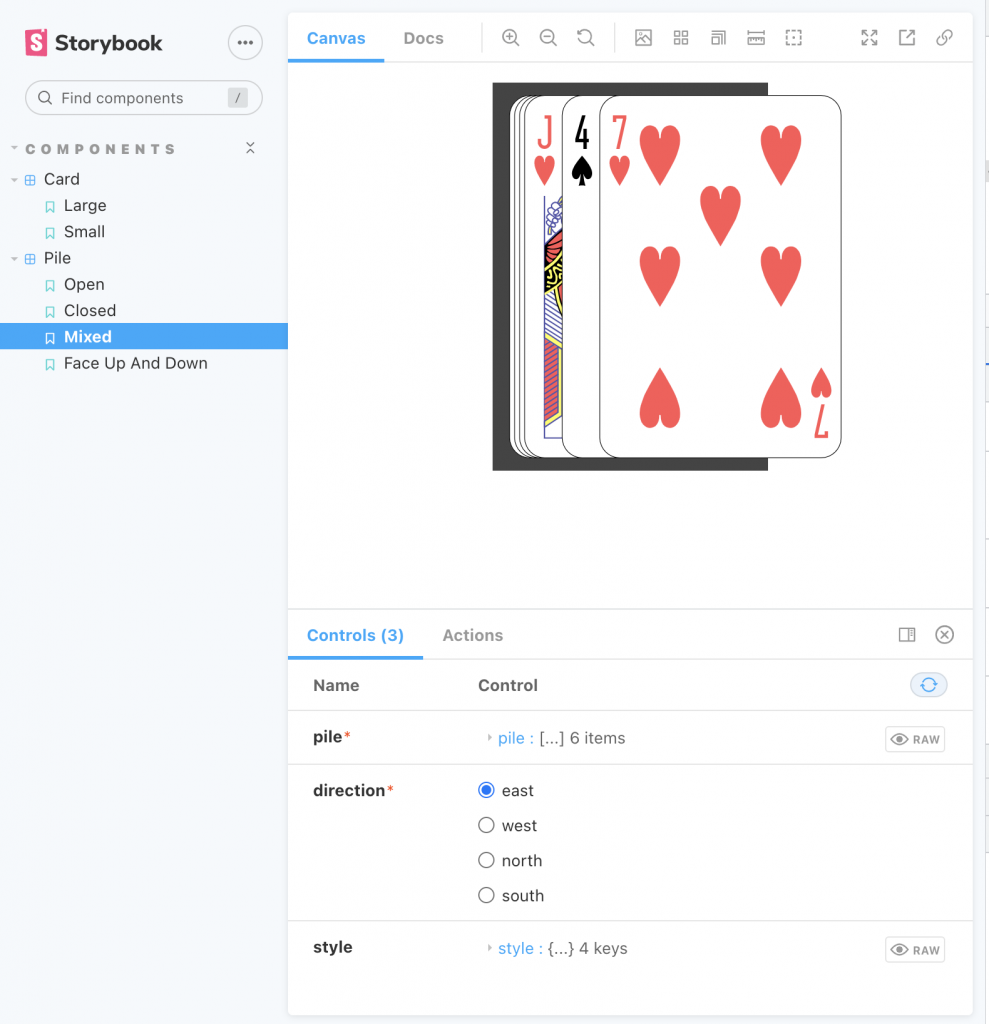
};This is what the resulting tableau looks like in Storybook.

Storybook view of the Tableau Component.
Next Steps
Now that the main components have been implemented, the next step is to create a class that will drive the Solitaire gameplay. This class will specify where the piles are located on the tableau and how they behave. The aim is to make this game model very general and driven by a data structure that defines the rules of the game. By exchanging the data, different games can be created easily without writing new code.
Fifty Solitaires – The Upgrade
Posted 5th October 2023 by Holger Schmitz
It has been well over a year since I last posted about this project. I have been busy with other projects and had to leave this one on the back burner. A lot has changed since then and the first thing that I noticed when looking at this project again was that I now needed to upgrade all the project’s dependencies to their latest versions. This might not be very interesting from a software development perspective, but it is a necessary step to ensure that the project is up to date. So, this post will be all about upgrading dependencies, making adjustments to the configuration and fixing any issues that might arise.
Attempting to run the last version of the project
Before I started upgrading dependencies, I wanted to make sure that the project still worked as expected. So, I cloned the repository and ran the following commands.
npm installRight away, I got error messages from node-gyp.js when it was trying to build the binaries of node-sass. I have seen this error before and it is usually caused by the fact that the version of node-sass is not compatible with the version of Node.js that I am using. So, I checked that I currently have Node.js version 20.5.1 installed and then I checked the node-sass documentation to see that I need version 9.0.0 of node-sass. So, I updated the package.json file to use the current latest version.
"node-sass": "^9.0.0",Remember that I had already created some components and stories for Storybook, but I had not yet implemented the main application. So, I ran Storybook to see if the components would still show up as expected.
npm run storybookStorybook uses Webpack 4 to bundle the project. This emitted the following error message
Error: error:0308010C:digital envelope routines::unsupportedAgain, this is a compatibility problem with Node. On StackOverflow, I found a solution that suggested telling Node.js to enable the legacy openssl provider. This can be done by setting an environment variable.
export NODE_OPTIONS=--openssl-legacy-provider
npm run storybookThis time, Storybook started up and I could see the project in the browser. At this point, I am hoping this environment variable will not be needed once I have upgraded all the dependencies. But for now, I will leave it in place.
Upgrading dependencies
Now that I can see the Card and Pile components in Storybook, I will start upgrading the dependencies. I had two options. Either I could try to update one dependency at a time and then run Storybook each time to see if it still worked. Or I could update all the dependencies at once and then fix any issues that might arise. The problem with the first approach is that some upgrades might not be independent of each other. This could create more work, trying to figure out all the errors in the intermediate stages that wouldn’t have occurred if I had just upgraded everything at once. So, I decided to go with the second approach. To do this, I removed all entries dependencies from the package.json file. I made a note of all the packages so that I could reinstall them later.
"dependencies": {},To reinstall all the packages, I first removed the node_modules folder and the package-lock.json file. Then I ran npm install with all the packages I had noted down from the dependencies section of the package.json file.
rm -rf node_modules package-lock.json
npm install @testing-library/jest-dom @testing-library/react \
@testing-library/user-event @types/jest @types/node @types/react \
@types/react-dom react node-sass react-dom react-scripts \
typescript web-vitalsNote, that I did not touch the devDependencies entry in packages.json. Looking at those entries, I saw that devDependencies only contains packages related to Storybook. This will be upgraded in a separate step. To test that the React application was still working, I ran the following command.
npm startThis worked fine. Of course, the application is only showing the default React page. Previously, I had not yet added anything to the front page because I was first focusing on creating the Card and Pile components and their Storybook stories. So, now it was time to upgrade Storybook. Fortunately, Storybook provides a command that can perform this task for you. From the documentation, I found that I should run the following command to upgrade Storybook.
npx storybook@latest upgradeThis prompted me with several questions about which migrations to run. I answered y to all of them. This step completed without any problems.
Fixing Remaining Issues
Now, it was time to check if the upgrade of Storybook had caused any issues. I ran the following command.
npm run storybookStorybook starts but then crashes. In the browser, I could only see the spinner. In the terminal, I was getting an extremely long error message that contained the full contents of my playing-cards.svg file. At the top of the error message, I see the following information.
SyntaxError: unknown: Namespace tags are not supported by default. React's JSX doesn't support namespace tags. Putting this error message into Google helped. This StackOverflow post helped me figure it out. My SVG file contains quite a few namespace tags but React does not understand namespace tags. By renaming them with a camel-cased variant I was able to get rid of the error. This was a bit tedious, but it did the trick. I am not quite sure why this was working before, but I am glad I was able to fix it.
Final Thoughts
After completing all the steps above, Storybook worked again. To double-check, I also opened a new terminal and tested Storybook without setting the NODE_OPTIONS environment variable. This means the intermediate fix for the legacy openssl provider was no longer necessary.
In conclusion, I was dreading the upgrade of the project’s dependencies. But apart from a few glitches, it turned out to be not too hard. In a previous attempt, I did not use the Storybook command and, instead, tried to upgrade Storybook manually. This did not work out so well. It shows how important it is to spend some time studying the documentation of the tools that you are using.
Computational Physics Basics: Polynomial Interpolation
Posted 19th April 2023 by Holger Schmitz
The piecewise constant interpolation and the linear interpolation seen in the previous post can be understood as special cases of a more general interpolation method. Piecewise constant interpolation constructs a polynomial of order 0 that passes through a single point. Linear interpolation constructs a polynomial of order 1 that passes through 2 points. We can generalise this idea to construct a polynomial of order \(n-1\) that passes through \(n\) points, where \(n\) is 1 or greater. The idea is that a higher-order polynomial will be better at approximating the exact function. We will see later that this idea is only justified in certain cases and that higher-order interpolations can actually increase the error when not applied with care.
Existence
The first question that arises is the following. Given a set of \(n\) points, is there always a polynomial of order \(n-1\) that passes through these points, or are there multiple polynomials with that quality? The first question can be answered simply by constructing a polynomial. The simplest way to do this is to construct the Lagrange Polynomial. Assume we are given a set of points, \[
(x_1, y_1), (x_2, y_2) \ldots (x_n, y_n),
\] where all the \(x\)’s are different, i.e. \(x_i \ne x_j\) if \(i \ne j\). Then we observe that the fraction \[
\frac{x – x_j}{x_i – x_j}
\] is zero when \(x = x_j\) and one when \(x = x_i\). Next, let’s choose an index \(i\) and multiply these fractions together for all \(j\) that are different to \(i\), \[
a_i(x) = \frac{x – x_1}{x_i – x_1}\times \ldots\times\frac{x – x_{i-1}}{x_i – x_{i-1}}
\frac{x – x_{i+1}}{x_i – x_{i+1}}\times \ldots\times\frac{x – x_n}{x_i – x_n}.
\] This product can be written a bit more concisely as \[
a_i(x) = \prod_{\stackrel{j=1}{j\ne i}}^n \frac{x – x_j}{x_i – x_j}.
\] You can see that the \(a_i\) are polynomials of order \(n-1\). Now, if \(x = x_i\) all the factors in the product are 1 which means that \(a_i(x_i) = 1\). On the other hand, if \(x\) is any of the other \(x_j\) then one of the factors will be zero and \(a_i(x_j) = 0\) for any \(j \ne i\). Thus, if we take the product \(a_i(x) y_i\) we have a polynomial that passes through the point \((x_i, y_i)\) but is zero at all the other \(x_j\). The final step is to add up all these separate polynomials to construct the Lagrange Polynomial, \[
p(x) = a_1(x)y_1 + \ldots a_n(x)y_n = \sum_{i=1}^n a_i(x)y_i.
\] By construction, this polynomial of order \(n-1\) passes through all the points \((x_i, y_i)\).
Uniqueness
The next question is if there are other polynomials that pass through all the points, or is the Lagrange Polynomial the only one? The answer is that there is exactly one polynomial of order \(n\) that passes through \(n\) given points. This follows directly from the fundamental theorem of algebra. Imagine we have two order \(n-1\) polynomials, \(p_1\) and \(p_2\), that both pass through our \(n\) points. Then the difference, \[
d(x) = p_1(x) – p_2(x),
\] will also be an order \(n-1\) degree polynomial. But \(d\) also has \(n\) roots because \(d(x_i) = 0\) for all \(i\). But the fundamental theorem of algebra asserts that a polynomial of degree \(n\) can have at most \(n\) real roots unless it is identically zero. In our case \(d\) is of order \(n-1\) and should only have \(n-1\) roots. The fact that it has \(n\) roots means that \(d \equiv 0\). This in turn means that \(p_1 = p_2\) must be the same polynomial.
Approximation Error and Runge’s Phenomenon
One would expect that the higher order interpolations will reduce the error of the approximation and that it would always be best to use the highest possible order. One can find the upper bounds of the error using a similar approach that I used in the previous post on linear interpolation. I will not show the proof here, because it is a bit more tedious and doesn’t give any deeper insights. Given a function \(f(x)\) over an interval \(a\le x \le b\) and sampled at \(n+1\) equidistant points \(x_i = a + hi\), with \(i=0, \ldots , n+1\) and \(h = (b-a)/n\), then the order \(n\) Lagrange polynomial that passes through the points will have an error given by the following formula. \[
\left|R_n(x)\right| \leq \frac{h^{n+1}}{4(n+1)} \left|f^{(n+1)}(x)\right|_{\mathrm{max}}
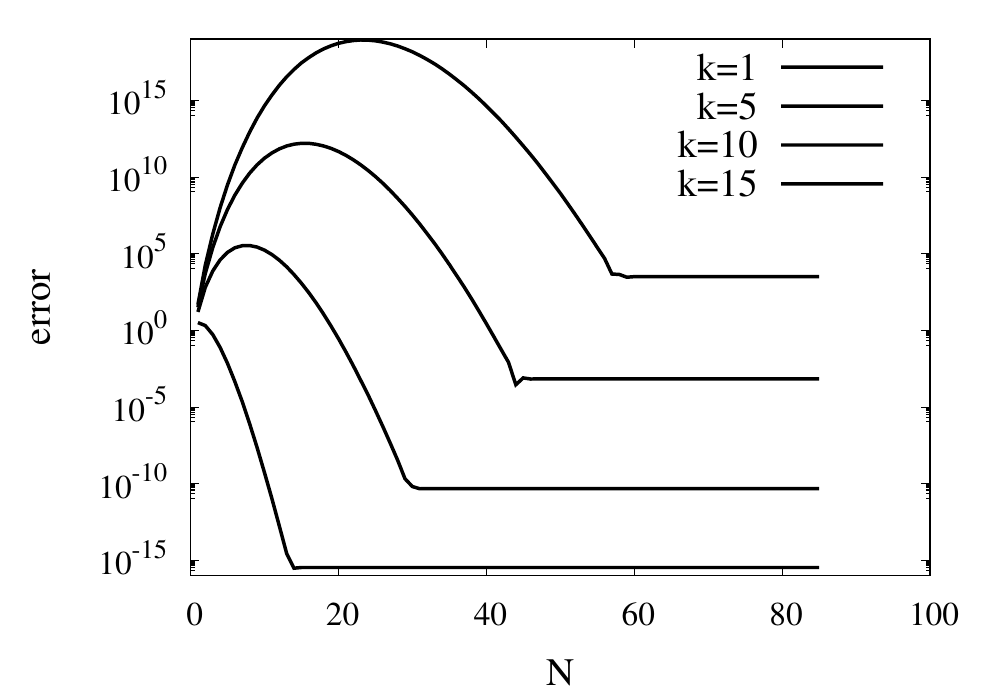
\] Here \(f^{(n+1)}(x)\) means the \((n+1)\)th derivative of the the function \(f\) and the \(\left|.\right|_{\mathrm{max}}\) means the maximum value over the interval between \(a\) and \(b\). As expected, the error is proportional to \(h^{n+1}\). At first sight, this implies that increasing the number of points, and thus reducing \(h\) while at the same time increasing \(n\) will reduce the error. The problem arises, however, for some functions \(f\) whose \(n\)-th derivatives grow with \(n\). The example put forward by Runge is the function \[
f(x) = \frac{1}{1+25x^2}.
\]
Interpolation of Runge’s function using higher-order polynomials.
The figure above shows the Lagrange polynomials approximating Runge’s function over the interval from -1 to 1 for some orders. You can immediately see that the approximations tend to improve in the central part as the order increases. But near the outermost points, the Lagrange polynomials oscillate more and more wildly as the number of points is increased. The conclusion is that one has to be careful when increasing the interpolation order because spurious oscillations may actually degrade the approximation.
Piecewise Polynomial Interpolation
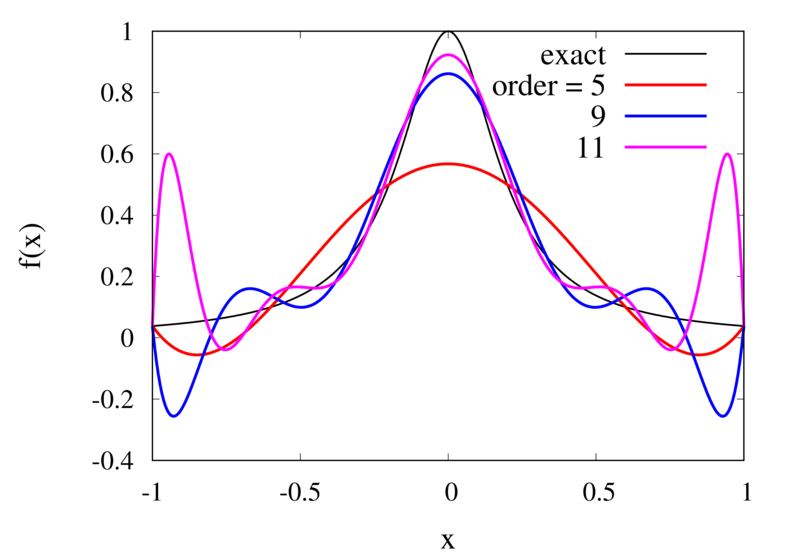
Does this mean we are stuck and that moving to higher orders is generally bad? No, we can make use of higher-order interpolations but we have to be careful. Note, that the polynomial interpolation does get better in the central region when we decrease the spacing between the points. When we used piecewise linear of constant interpolation, we chose the points that were used for the interpolation based on where we wanted to interpolate the function. In the same way, we can choose the points through which we construct the polynomial so that they are always symmetric around \(x\). Some plots of this piecewise polynomial interpolation are shown in the plot below.
Piecewise Lagrange interpolation with 20 points for orders 0, 1, 2, and 3.
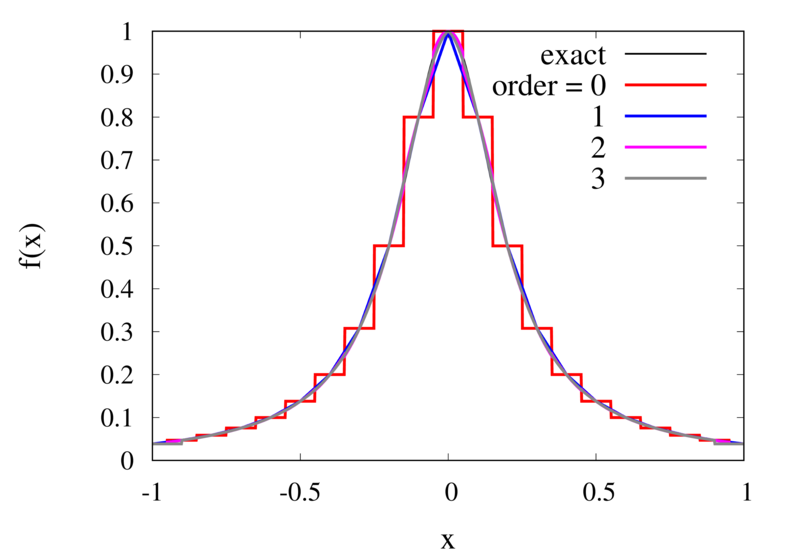
Let’s analyse the error of these approximations. Using an array with \(N\) points on Runge’s function equally spaced between -2 and 2. \(N\) was varied between 10 and 10,000. For each \(N\), the centred polynomial interpolation of orders 0, 1, 2, and 3 was created. Finally, the maximum error of the interpolation and the exact function over the interval -1 and 1 are determined.
Scaling of the maximum error of the Lagrange interpolation with the number of points for increasing order.
The plot above shows the double-logarithmic dependence of the error against the number of points for each order interpolation. The slope of each curve corresponds to the order of the interpolation. For the piecewise constant interpolation, an increase in the number of points by 3 orders of magnitude also corresponds to a reduction of the error by three orders of magnitude. This indicates that the error is first order in this case. For the highest order interpolation and 10,000 points, the error reaches the rounding error of double precision.
Discontinuities and Differentiability
As seen in the previous section, for many cases the piecewise polynomial interpolation can provide a good approximation to the underlying function. However, in some cases, we need to use the first or second derivative of our interpolation. In these cases, the Lagrange formula is not ideal. To see this, the following image shows the interpolation error, again for Runge’s function, using order 2 and 3 polynomials and 20 points.
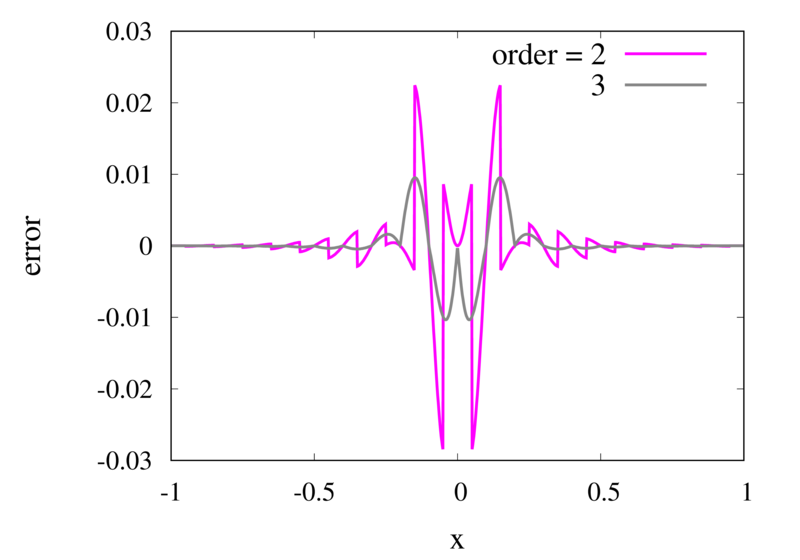
Error in the Lagrange interpolation of Runge’s function for orders 2 and 3.
One can see that the error in the order 2 approximation has discontinuities and the error in the order 3 approximation has discontinuities of the derivative. For odd-order interpolations, the points that are used for the interpolation change when \(x\) moves from an interval \([x_{i-1},x_i]\) to an interval \([x_i, x_{i+1}]\). Because both interpolations are the same at the point \(x_i\) itself, the interpolation is continuous but the derivative, in general, is not. For even-order interpolations, the stencil changes halfway between the points, which means that the function is discontinuous there. I will address this problem in a future post.
Starting GPU programming with Kokkos
Posted 9th March 2023 by Holger Schmitz
The high performance computing landscape has changed quite a bit over the last years. For quite a few decades, the major architecture for HPC systems was based on classical CPU processors distributed over many nodes. The nodes are connected via a fast network architecture. These compute clusters have evolved over time. A typical simulation code that makes use of this architecture will consist of more or less serial code that runs on each core and communicates with the other cores via the message passing library MPI. This has the drawback that the serial instances of the simulation code running on a shared memory node still have to exchange data through this mechanism, which takes time and reduces efficiency. On many current systems, each node can have on the order of 10s of compute cores accessing the same shared memory. To make better use of these cores, multithreading approaches, such as OpenMP, have been used increasingly over the past decade or so. However, there are not many large scale simulation codes that make use of OpenMP and MPI at the same time to reach maximum performance.
More recently, there has been new style of architecture that has become a serious player. GPU processors that used to play more of an outsider role in serious high performance computing have taken centre stage. Within the DoE’s Exascale project in the US, new supercomputers are being built that are breaking the exaflop barrier. These machines rely on a combination of traditional CPU cluster with GPU accelerators.
For developers of high performance simulation codes this means that much of their code has to be re-written to make use of the new mixed architectures. I have been developing the Schnek library for a number of years now and I am using it form many of my simulation codes. To keep the library relevant for the future, I am currently in the process of adding mixed architecture capabilities to Schnek. Fortunately, there already exists the Kokkos library which provides an abstraction layer over the different machine architectures. It also provides multi-dimensional arrays that can be stored on the host memory or on the accelerator’s device memory. It also provides iteration mechanisms to process these arrays on the CPU or GPU.
In this post, I am describing my first experiences with Kokkos and how it can be used to accelerate calculations. I will be starting from scratch which means that I will begin by installing Kokkos. The best way to do this nowadays is to use a packet manager called Spack. Spack is designed as a packet manager for supercompters but will work on any regular Linux machine. To start, I navigate into a folder where I want to install spack, let’s call it /my/installation/folder. I then simply clone Spack’s git repository.
git clone -c feature.manyFiles=true https://github.com/spack/spack.gitI am using the bash shell, so now I can initialise all the environment variables by running
source /my/installation/folder/spack/share/spack/setup-env.shThis command should be run every time you want to start developing code using the packages supplied by Spack. I recommend not putting this line into your .bashrc because some of the Spack packages might interfere with your regular system operation.
The Kokkos package has many configuration options. You can now look at them using the command
spack info kokkosI have an NVidia Quadro P1000 graphics card on my local development machine. For NVidia accelerators, I will need to install Kokkos with Cuda support. In order to install the correct Cuda version, I first check on https://developer.nvidia.com/cuda-gpus for the compute capability. For my hardware, I find that I will need version 6.1. The following command will install Kokkos and all of its dependencies.
spack install kokkos +cuda +wrapper cuda_arch=61The wrapper option is required because I am compiling everything with the gcc compiler. Note that this can take quite some time because many of the packages may be build from source code during the installation. This allows Spack packages to be highly specific to your system.
spack load kokkosNow, I can start creating my first Kokkos example. I create a file called testkokkos.cpp and add some imports to the top.
#include <Kokkos_Core.hpp>
#include <chrono>The Kokkos_Core.hpp import is needed to use Kokkos and I also included chrono from the standard library to allow timing the code. Kokkos introduces execution spaces and memory spaces. Data can live on the host machine or the accelerator device. Similarly, execution of the code can be carried out on the serial CPU or the GPU or some other specialised processor. I want my code to be compiled for two different settings so that I can compare GPU performance against the CPU. I define two types Execution and Memory for the execution and memory spaces. These types will depend on an external macro that will be passed in by the build system.
#ifdef TEST_USE_GPU
typedef Kokkos::Cuda Execution;
typedef Kokkos::CudaSpace Memory;
#else
typedef Kokkos::Serial Execution;
typedef Kokkos::HostSpace Memory;
#endifKokkos manages data in View objects which represent multi-dimensional arrays. View has some template arguments. The first argument specifies the dimensionality and the datatype stored in the array. Further template arguments can be specified to specify the memory space and other compile-time configurations. For example Kokkos::View<double**, Kokkos::HostSpace> defines a two dimensional array of double precision values on the host memory. To iterate over a view, one needs to define function objects that will be passed to a function that Kokkos calls “parallel dispatch”. The following code defines three such structs that can be used to instantiate function objects.
#define HALF_SIZE 500
struct Set {
Kokkos::View<double**, Memory> in;
KOKKOS_INLINE_FUNCTION void operator()(int i, int j) const {
in(i, j) = i==HALF_SIZE && j==HALF_SIZE ? 1.0 : 0.0;
}
};
struct Diffuse {
Kokkos::View<double**, Memory> in;
Kokkos::View<double**, Memory> out;
KOKKOS_INLINE_FUNCTION void operator()(int i, int j) const {
out(i, j) = in(i, j) + 0.1*(in(i-1, j) + in(i+1, j) + in(i, j-1) + in(i, j+1) - 4.0*in(i, j));
}
};The Set struct will initialise an array to 0.0 everywhere except for one position where it will be set to 1.0. This results in a single spike in the centre of the domain. Diffuse applies a diffusion operator to the in array and stored the result in the out array. The calculations can’t be carried out in-place because the order in which the function objects are called may be arbitrary. This means that, after the diffusion operator has been applied, the values should be copied back from the out array to the in array.
Now that these function objects are defined, I can start writing the actual calculation.
void performCalculation() {
const int N = 2*HALF_SIZE + 1;
const int iter = 100;
Kokkos::View<double**, Memory> in("in", N, N);
Kokkos::View<double**, Memory> out("out", N, N);
Set set{in};
Diffuse diffuse{in, out};The first two line in the function define some constants. N is the size of the grids and iter sets the number of times that the diffusion operator will be applied. The Kokkos::View objects in and out store the 2-dimensional grids. The first template argument double ** specifies that the arrays are 2-dimensional and store double values. The Memory template argument was defined above and can either be Kokkos::CudaSpace or Kokkos::HostSpace. The last two lines in the code segment above initialise my two function objects of type Set and Diffuse.
I want to iterate over the inner domain, excluding the grid points at the edge of the arrays. This is necessary because the diffusion operator accesses the grid cells next to the position that is iterated over. The iteration policy uses the multidmensional range policy from Kokkos.
auto policy = Kokkos::MDRangePolicy<Execution, Kokkos::Rank<2>>({1, 1}, {N-1, N-1});The Execution template argument was defined above and can either be Kokkos::Cuda or Kokkos::Serial. The main calculation now looks like this.
Kokkos::parallel_for("Set", policy, set);
Kokkos::fence();
auto startTime = std::chrono::high_resolution_clock::now();
for (int i=0; i<iter; ++i)
{
Kokkos::parallel_for("Diffuse", policy, diffuse);
Kokkos::fence();
Kokkos::deep_copy(in, out);
}
auto endTime = std::chrono::high_resolution_clock::now();
auto milliseconds = std::chrono::duration_cast<std::chrono::milliseconds>(endTime - startTime).count();
std::cerr << "Wall clock: " << milliseconds << " ms" << std::endl;
}The function Kokkos::parallel_for applies the function object for each element given by the iteration policy. Depending on the execution space, the calculations are performed on the CPU or the GPU. To set up the calculation the set operator is applied. Inside the main loop, the diffusion operator is applied, followed by a Kokkos::deep_copy which copies the out array back to the in array. Notice, that I surrounded the loop by calls to STL’s high_resolution_clock::now(). This will allow me to print out the wall-clock time used by the calculation and give me some indication of the performance of the code.
The main function now looks like this.
int main(int argc, char **argv) {
Kokkos::initialize(argc, argv);
performCalculation();
Kokkos::finalize_all();
return 0;
}It is important to initialise Kokkos before any calls to its routines are called, and also to finalise it before the program is exited.
To compile the code, I use CMake. Kokkos provides the necessary CMake configuration files and Spack sets all the paths so that Kokkos is easily found. My CMakeLists.txt file looks like this.
cmake_minimum_required(VERSION 3.10)
project(testkokkos LANGUAGES CXX)
set(CMAKE_CXX_STANDARD 17)
set(CMAKE_CXX_STANDARD_REQUIRED ON)
set(CMAKE_CXX_EXTENSIONS OFF)
set(CMAKE_ARCHIVE_OUTPUT_DIRECTORY ${CMAKE_BINARY_DIR}/lib)
set(CMAKE_LIBRARY_OUTPUT_DIRECTORY ${CMAKE_BINARY_DIR}/lib)
set(CMAKE_RUNTIME_OUTPUT_DIRECTORY ${CMAKE_BINARY_DIR}/bin)
find_package(Kokkos REQUIRED PATHS ${KOKKOS_DIR})
# find_package(CUDA REQUIRED)
add_executable(testkokkosCPU testkokkos.cpp)
target_compile_definitions(testkokkosCPU PRIVATE KOKKOS_DEPENDENCE)
target_link_libraries(testkokkosCPU PRIVATE Kokkos::kokkoscore)
add_executable(testkokkosGPU testkokkos.cpp)
target_compile_definitions(testkokkosGPU PRIVATE TEST_USE_GPU KOKKOS_DEPENDENCE)
target_link_libraries(testkokkosGPU PRIVATE Kokkos::kokkoscore)Running cmake . followed by make will build two targets, testkokkosCPU and testkokkosGPU. In the compilation of testkokkosGPU the TEST_USE_GPU macro has been set so that it will make use of the Cuda memory and execution spaces.
Now its time to compare. Running testkokkosCPU writes out
Wall clock: 9055 msRunning it on the GPU with testkokkosGPU gives me
Wall clock: 57 msThat’s right! On my NVidia Quadro P1000, the GPU accelerated code outperforms the serial version by a factor of more than 150.
Using Kokkos is a relatively easy and very flexible way to make use of GPUs and other accelerator architectures. As a developer of simulation codes, the use of function operators may seem a bit strange at first. From a computer science perspective, on the other hand, these operators feel like a very natural way of approaching the problem.
My next task now is to integrate the Kokkos approach with Schnek’s multidimensional grids and fields. Fortunately, Schnek provides template arguments that allow fine control over the memory model and this should allow replacing Schnek’s default memory model with Kokkos views.
Fifty Solitaires – Piling it Up
Posted 16th March 2022 by Holger Schmitz
So here is the third instalment of my Solitaire card game. In the previous post, I created the basic Card component and set up Storybook to let me browse and test my components while developing them. Today, I will create another component that displays a collection of cards. In a Solitaire game, cards are arranged on the table in piles. The cards in the piles can be face-up or face-down. In addition, piles can be closed or open. In closed piles, each card is placed exactly on top of the previous one. In open piles, each card is placed slightly offset from the one beneath. For face-up cards, this allows the player to see the suit and value of each card in the pile. For face-down cards, it lets the player see easily how many cards are in the pile.
Face-down cards
The Card component that I created in the previous post did not allow for face-down cards. So, let’s first add the face-down feature to the existing component. The first step is to create a face-down card symbol in the SVG file that contains all the other cards. In src/assets/playing_cards.svg, I added the following symbol before the closing </svg> tag.
<symbol id="face-down" viewBox="30 2310 360 540">
<g
transform="translate(30,1797.6378)"
id="face-down">
<rect
rx="29.944447"
ry="29.944447"
y="512.86218"
x="0.5"
height="539"
width="359"
id="rect6472-45"
style="fill:#ffffff;stroke:#000000;stroke-width:0.99999976" />
<rect
rx="19.944447"
ry="19.944447"
y="532.86218"
x="20.5"
height="499"
width="319"
id="rect6472-45"
style="fill:none; stroke:#000088; stroke-width:5" />
<rect
rx="9.944447"
ry="9.944447"
y="552.86218"
x="40.5"
height="459"
width="279"
id="rect6472-45"
style="fill:none; stroke:#000088; stroke-width:5" />
</g>
</symbol>I tried to set the parameters of the ViewBox and the transform attributes in line with all the other symbols in the file. The face-down symbol simply consists of a white background with two rounded rectangles inside. It is probably not the most beautiful reverse side of a playing card but, given that I coded the SVG by hand, it will have to do for now.
Next, I amended the Card component in src/components/Card.tsx to allow a faceUp property to be passed in. If faceUp is true the card will be displayed as usual, and if it is false the face-down symbol will be shown. I also changed the CardProperties type to allow additional properties to be passed in.
export interface CardData {
suit: CardSuit;
value: CardValue;
faceUp: boolean;
}
export interface CardProperties extends React.SVGProps<SVGSVGElement>, CardData {}
export function Card({suit, value, faceUp, ...props}: CardProperties) {
const cardId = faceUp
? `${playingCards}#${value.toLowerCase()}-${suit.toLowerCase()}`
: `${playingCards}#face-down`;
const classNames = `${props.className} card-component`;
return <svg {...props} className={classNames} >
<use xlinkHref={cardId}></use>
</svg>
}To be able to test the new feature in Storybook, I added a faceUp: true property to the existing stories in src/stories/Card.stories.tsx. This automatically adds a switch in the Storybook stories that toggle the face-down/face-up status.
Creating the Pile
Next, I created a new component in src/components/Pile.tsx. This file contains a few bits, so I will go through it piece by piece. At the top of the file, I do some imports and type definitions.
import { Card, CardData } from "./Card";
import './Pile.css'
export interface CardDisplayProperties extends CardData {
open: boolean;
}
export type PileData = Array<CardDisplayProperties>;
export enum Direction {
east = 'east',
west = 'west',
north = 'north',
south = 'south'
}
export interface PileProperties {
pile: PileData;
direction: Direction;
}First, I imported the Card component as well as a CSS stylesheet that I yet have to create. The CardDisplayProperties interface contains all the data needed to show a card on the pile. In addition to the CardData, it contains an open flag to control if the position of the card is offset from the card below it. The PileData type is then simply an array of CardDisplayProperties. I also wanted to allow the direction of the offset to be controlled. I remember that some Solitaire variants have piles that fan out to the left or right. I just want to be prepared for this. So, I created a Direction enum that contains the four directions of the compass. Finally, the PileProperties interface is made up of the pile data and a direction.
To position the cards, the idea is to use a <div> and use absolute positioning and then place the individual cards. Each card will have a different offset from the top or left, depending on how many open and closed cards have already been placed below it. Before I continue with the code in Pile.jsx, let me first show you the CSS style in src/components/Pile.css
.card-pile {
position: relative;
overflow: visible;
width: 100%;
height: 100%;
}
.card-pile .card {
position: absolute;
top: 0;
left: 0;
}The .card-pile class will be used for the Pile component and the .card is the CSS class of the Card component within a pile. The overflow: visible is needed so that cards can freely be placed outside the original bounding box of the pile which should just be the size of the bottom card in the pile. You can see that the top and left properties of the cards default to zero but they can be overwritten by inline styles.
Next, in src/components/Pile.tsx I defined a helper object called margins.
const margins: {[key: string]: [string, number, number]} = {
east: [ 'left', 15, 2],
west: [ 'left', -15, -2],
north: [ 'top', -15, -2],
south: [ 'top', 15, 2],
}The object is meant to serve as a look-up from the Direction enum to an array of parameters. The first entry in the array determines the CSS property that needs to be modified, the second entry is the percentage offset for open cards, and the third entry is the percentage offset for closed cards.
Now, I am ready to create the Pile component.
export function Pile({pile, direction}: PileProperties) {
const marginSpec = margins[direction];
return <div className={`card-pile card-pile-${direction}`}>
{pile.map(function cardMapper(this: {offset: number}, card, index) {
const cardStyle = {
[marginSpec[0]]: `${this.offset}%`
}
this.offset += card.open ? marginSpec[1] : marginSpec[2];
return <Card
className={`card ${card.open ? 'open' : ''}`}
suit={card.suit}
value={card.value}
faceUp={card.faceUp}
key={index}
style={cardStyle} />
}, {offset: 0})}
</div>
}The first line chooses the margin specifications from the margins dictionary based on the pile direction. Then inside the outer <div> the pile array is mapped to an array of Card components. I am using a less well-known feature of the Array.map function by passing {offset: 0} as a second argument after the mapper function. This argument will be attached to this inside the mapper callback. To make this work, I have to make sure that two conditions are met. First, I have to use the function keyword for the callback. This ensures that the callback has a this reference. Second, for Typescript to know the type of this, the callback function takes this as a first argument. This is compiled away in the transformation from Typescript to JavaScript and is only there to make the Typescript type system aware that this.offset exists. The offset property itself is incremented depending on the card.open flag and the margin specification.
The Story for the Pile
Now that we have completed the Pile component, we want to make it show up in Storybook as well. What follows is a slightly lengthy file that contains three stories and is stored in src/stories/Pile.stories.tsx.
import { Pile, PileProperties } from '../components/Pile';
import { CardSuit, CardValue } from '../components/Card';
export default {
component: Pile,
title: 'Components/Pile',
};
interface StoryPileProperties extends PileProperties {
style: { [key: string]: string}
}
function Template(args: StoryPileProperties) {
return <div style={({
display: 'flex',
justifyContent: "center",
width: "100%",
})}>
<div style={args.style}><Pile {...args} /></div>
</div>
};
export const Open = Template.bind({});
(Open as any).args = {
pile: [
{ suit: CardSuit.clubs, value: CardValue.ace, faceUp: true, open: true },
{ suit: CardSuit.clubs, value: CardValue.three, faceUp: true, open: true },
{ suit: CardSuit.diamonds, value: CardValue.eight, faceUp: true, open: true },
],
direction: 'south',
style: {
width: 200,
height: 290,
backgroundColor: '#444444',
padding: 10
}
};
export const Closed = Template.bind({});
(Closed as any).args = {
pile: [
{ suit: CardSuit.clubs, value: CardValue.ace, faceUp: true, open: false },
{ suit: CardSuit.clubs, value: CardValue.three, faceUp: true, open: false },
{ suit: CardSuit.diamonds, value: CardValue.eight, faceUp: true, open: false },
],
direction: 'south',
style: {
width: 200,
height: 290,
backgroundColor: '#444444',
padding: 10
}
};
export const Mixed = Template.bind({});
(Mixed as any).args = {
pile: [
{ suit: CardSuit.clubs, value: CardValue.ace, faceUp: true, open: false },
{ suit: CardSuit.clubs, value: CardValue.three, faceUp: true, open: false },
{ suit: CardSuit.diamonds, value: CardValue.eight, faceUp: true, open: false },
{ suit: CardSuit.hearts, value: CardValue.jack, faceUp: true, open: true },
{ suit: CardSuit.spades, value: CardValue.four, faceUp: true, open: true },
{ suit: CardSuit.hearts, value: CardValue.seven, faceUp: true, open: true },
],
direction: 'south',
style: {
width: 200,
height: 290,
backgroundColor: '#444444',
padding: 10
}
};
export const FaceUpAndDown = Template.bind({});
(FaceUpAndDown as any).args = {
pile: [
{ suit: CardSuit.clubs, value: CardValue.ace, faceUp: false, open: true },
{ suit: CardSuit.clubs, value: CardValue.three, faceUp: false, open: true },
{ suit: CardSuit.spades, value: CardValue.four, faceUp: true, open: true },
{ suit: CardSuit.hearts, value: CardValue.seven, faceUp: true, open: true },
],
direction: 'south',
style: {
width: 200,
height: 290,
backgroundColor: '#444444',
padding: 10,
}
};There is nothing too fancy about this file. It defines a reusable Template to show the Pile component in some context. Then, each story is defined by the open and closed, and the face-up and face-down cards. I have created three stories showing different use cases. Now I can run
The image below shows an example of a pile feathered out to the east direction.
One of the stories for the Pile component in Storybook
Next Steps
Now that I have a Card component and a Pile component, I will need another component that arranges different piles on the table. This will most likely be the topic of my next post on the JavaScript Solitaire game. After that, I need to look into implementing a drag-and-drop mechanism so that the player can pick up cards from one pile and place them on another pile. When that’s done, I can start creating the game model that implements the rules of the Solitaire games.
Computational Physics Basics: Piecewise and Linear Interpolation
Posted 24th February 2022 by Holger Schmitz
One of the main challenges of computational physics is the problem of representing continuous functions in time and space using the finite resources supplied by the computer. A mathematical function of one or more continuous variables naturally has an infinite number of degrees of freedom. These need to be reduced in some manner to be stored in the finite memory available. Maybe the most intuitive way of achieving this goal is by sampling the function at a discrete set of points. We can store the values of the function as a lookup table in memory. It is then straightforward to retrieve the values at the sampling points. However, in many cases, the function values at arbitrary points between the sampling points are needed. It is then necessary to interpolate the function from the given data.
Apart from the interpolation problem, the pointwise discretisation of a function raises another problem. In some cases, the domain over which the function is required is not known in advance. The computer only stores a finite set of points and these points can cover only a finite domain. Extrapolation can be used if the asymptotic behaviour of the function is known. Also, clever spacing of the sample points or transformations of the domain can aid in improving the accuracy of the interpolated and extrapolated function values.
In this post, I will be talking about the interpolation of functions in a single variable. Functions with a higher-dimensional domain will be the subject of a future post.
Functions of a single variable
A function of a single variable, \(f(x)\), can be discretised by specifying the function values at sample locations \(x_i\), where \(i=1 \ldots N\). For now, we don’t require these locations to be evenly spaced but I will assume that they are sorted. This means that \(x_i < x_{i+1}\) for all \(i\). Let’s define the function values, \(y_i\), as \[
y_i = f(x_i).
\] The intuitive idea behind this discretisation is that the function values can be thought of as a number of measurements. The \(y_i\) provide incomplete information about the function. To reconstruct the function over a continuous domain an interpolation scheme needs to be specified.
Piecewise Constant Interpolation
The simplest interpolation scheme is the piecewise constant interpolation, also known as the nearest neighbour interpolation. Given a location \(x\) the goal is to find a value of \(i\) such that \[
|x-x_i| \le |x-x_j| \quad \text{for all} \quad j\ne i.
\] In other words, \(x_i\) is the sample location that is closest to \(x\) when compared to the other sample locations. Then, define the interpolation function \(p_0\) as \[
p_0(x) = f(x_i)
\] with \(x_i\) as defined above. The value of the interpolation is simply the value of the sampled function at the sample point closest to \(x\).
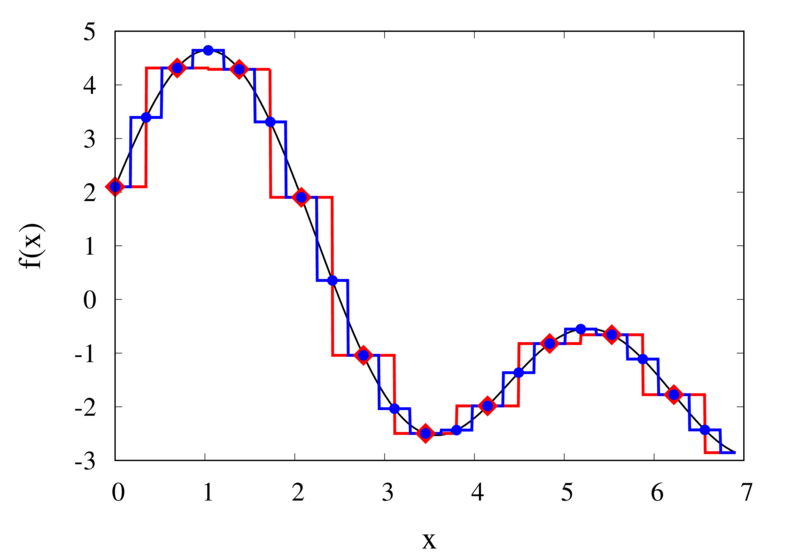
Piecewise constant interpolation of a function (left) and the error (right)
The left plot in the figure above shows some smooth function in black and a number of sample points. The case where 10 sample points are taken is shown by the diamonds and the case for 20 sample points is shown by the circles. Also shown are the nearest neighbour interpolations for these two cases. The red curve shows the interpolated function for 10 samples and the blue curve is for the case of 20 samples. The right plot in the figure shows the difference between the original function and the interpolations. Again, the red curve is for the case of 10 samples and the blue curve is for the case of 20 samples. We can see that the piecewise constant interpolation is crude and the errors are quite large.
As expected, the error is smaller when the number of samples is increased. To analyse exactly how big the error is, consider the residual for the zero-order interpolation \[
R_0(x) = f(x) – p_0(x) = f(x) – f(x_i).
\] The first step to analyse the magnitude of the residual is to perform a Taylor expansion of the residual around the point \(x_i\). We only need the zero order term. Using Taylor’s Theorem and the Cauchy form of the remainder, one can write \[
R_0(x) = \left[ f(x_i) + f'(\xi_c)(x – x_i)\right] – f(x_i).
\] The term in the brackets is the Taylor expansion of \(f(x)\), and \(\xi_c\) is some value that lies between \(x_i\) and \(x\) and depends on the value of \(x\). Let’s define the distance between two samples with \(h=x_{i+1}-x_i\). Assume for the moment that all samples are equidistant. It is not difficult to generalise the arguments for the case when the support points are not equidistant. This means, the maximum value of \(x – x_i\) is half of the distance between two samples, i.e. \[
x – x_i \le \frac{h}{2}.
\] It os also clear that \(f'(\xi_c) \le |f'(x)|_{\mathrm{max}}\), where the maximum is over the interval \(|x-x_i| \le h/2\). The final result for an estimate of the residual error is \[
|R_0(x)| \le\frac{h}{2} |f'(x)|_{\mathrm{max}}
\]
Linear Interpolation
As we saw above, the piecewise interpolation is easy to implement but the errors can be quite large. Most of the time, linear interpolation is a much better alternative. For functions of a single argument, as we are considering here, the computational expense is not much higher than the piecewise interpolation but the resulting accuracy is much better. Given a location \(x\), first find \(i\) such that \[
x_i \le x < x_{i+1}.
\] Then the linear interpolation function \(p_1\) can be defined as \[
p_1(x) = \frac{x_{i+1} – x}{x_{i+1} – x_i} f(x_i)
+ \frac{x – x_i}{x_{i+1} – x_i} f(x_{i+1}).
\] The function \(p_1\) at a point \(x\) can be viewed as a weighted average of the original function values at the neighbouring points \(x_i\) and \(x_{i+1}\). It can be easily seen that \(p(x_i) = f(x_i)\) for all \(i\), i.e. the interpolation goes through the sample points exactly.
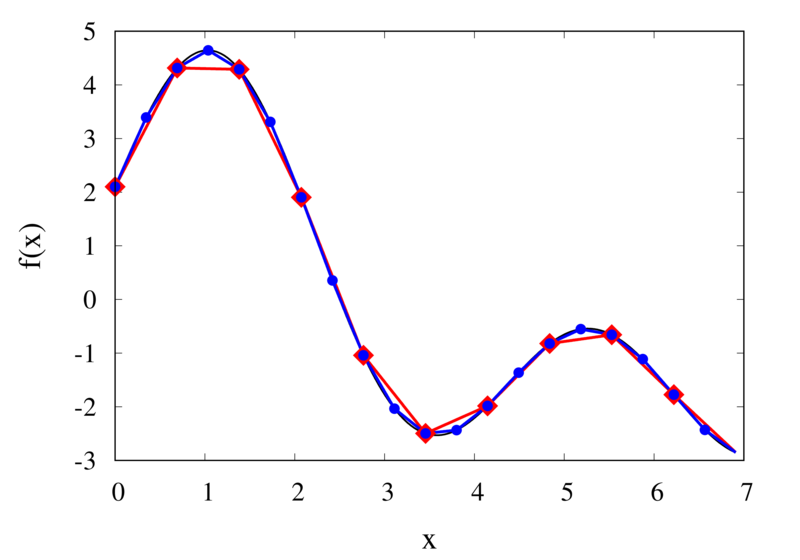
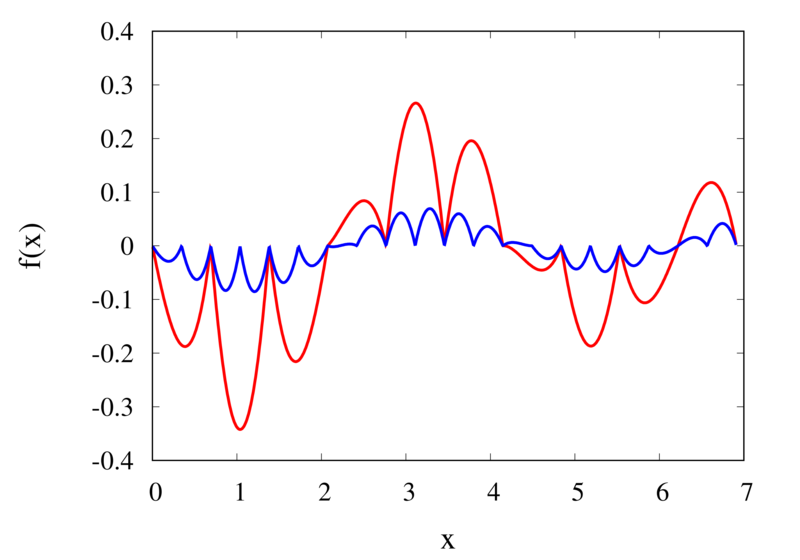
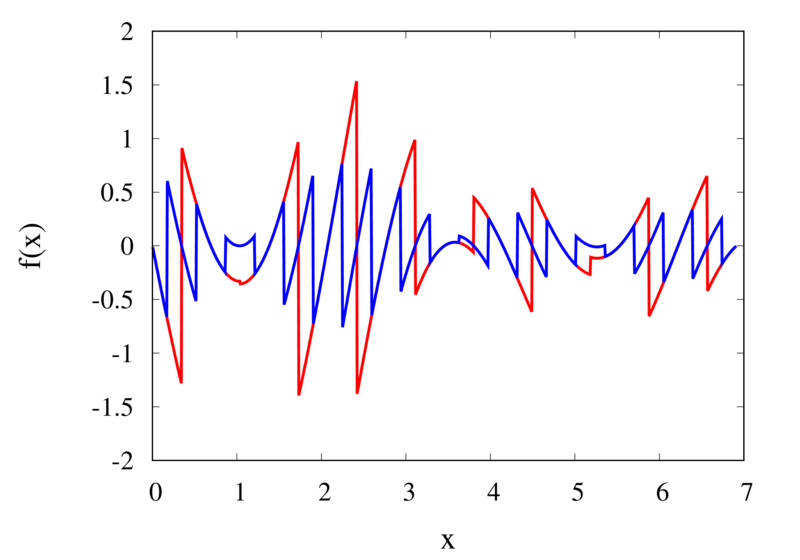
Linear interpolation of a function (left) and the error (right)
The left plot in the figure above shows the same function \(f(x)\) as the figure in the previous section but now together with the linear interpolations for 10 samples (red curve) and 20 samples (blue curve). One can immediately see that the linear interpolation resembles the original function much more closely. The right plot shows the error for the two interpolations. The error is much smaller when compared to the error for the piecewise interpolation. For the 10 sample interpolation, the maximum absolute error of the linear interpolation is about 0.45 compared to a value of over 1.5 for the nearest neighbour interpolation. What’s more, going from 10 to 20 samples improves the error substantially.
One can again try to quantify the error of the linear approximation using Taylor’s Theorem. The first step is to use the Mean Value Theorem that states that there is a point \(x_c\) between \(x_i\) and \(x_{i+1}\) that satisfies \[
f'(x_c) = \frac{ f(x_{i+1}) – f(x_i) }{ x_{i+1} – x_i }.
\] Consider now the error of the linear approximation, \[
R_1(x) = f(x) – p_1(x) = f(x) – \left[\frac{x_{i+1} – x}{x_{i+1} – x_i} f(x_i)
+ \frac{x – x_i}{x_{i+1} – x_i} f(x_{i+1})\right].
\] The derivative of the error is \[
R’_1(x) = f'(x) – \frac{ f(x_{i+1}) – f(x_i) }{ x_{i+1} – x_i }.
\] The Mean Value Theorem implies that the derivative of the error at \(x_c\) is zero and the error is at its maximum at that point. In other words, to estimate the maximum error, we only need to find an upper bound of \(|R(x_c)|\).
We now perform a Taylor expansion of the error around \(x_c\). Using again the Cauchy form of the remainder, we find \[
R(x) = R(x_c) + xR'(x_c) + \frac{1}{2}R’^\prime(\xi_c)(x-\xi_c)(x-x_c).
\] The second term on the right hand side is zero by construction, and we have \[
R(x) = R(x_c) + \frac{1}{2}R’^\prime(\xi_c)(x-\xi_c)(x-x_c).
\] Let \(h\) again denote the distance between the two points, \(h=x_{i+1} – x_i\). We assume that \(x_c – x_i < h/2\) and use the equation above to calculate \(R(x_i)\) which we know is zero. If \(x_c\) was closer to \(x_{i+1}\) we would have to calculate \(R(x_{i+1})\) but otherwise the argument would remain the same. So, \[
R(x_i) = 0 = R(x_c) + \frac{1}{2}R’^\prime(\xi_c)(x_i-\xi_c)(x_i-x_c)
\] from which we get \[
|R(x_c)| = \frac{1}{2}|R’^\prime(\xi_c)(x_i-\xi_c)(x_i-x_c)|.
\] To get an upper estimate of the remainder that does not depend on \(x_c\) or \(\xi_c\) we can use the fact that both \(x_i-\xi_c \le h/2\) and \(x_i-x_c \le h/2\). We also know that \(|R(x)| \le |R(x_c)|\) over the interval from \(x_i\) to \(x_{i+1}\) and \(|R’^\prime(\xi_c)| = |f’^\prime(\xi_c)| \le |f’^\prime(x)|_{\mathrm{max}}\). Given all this, we end up with \[
|R(x)| \le \frac{h^2}{8}|f’^\prime(x)|_{\mathrm{max}}.
\]
The error of the linear interpolation scales with \(h^2\), in contrast to \(h\) for the piecewise constant interpolation. This means that increasing the number of samples gives us much more profit in terms of accuracy. Linear interpolation is often the method of choice because of its relative simplicity combined with reasonable accuracy. In a future post, I will be looking at higher-order interpolations. These higher-order schemes will scale even better with the number of samples but this improvement comes at a cost. We will see that the price to be paid is not only a higher computational expense but also the introduction of spurious oscillations that are not present in the original data.
The Harmonic Oscillator
Posted 11th February 2022 by Holger Schmitz
I wasn’t really planning on writing this post. I was preparing a different post when I found that I needed to explain a property of the so-called “harmonic oscillator”. I first thought about adding a little excursion into the article that I was going to write. But I found that the harmonic oscillator is such an important concept in physics that it would not be fair to deny it its own post. The harmonic oscillator appears in many contexts and I don’t think there is any branch in physics that can do without it.
The Spring-and-Mass System
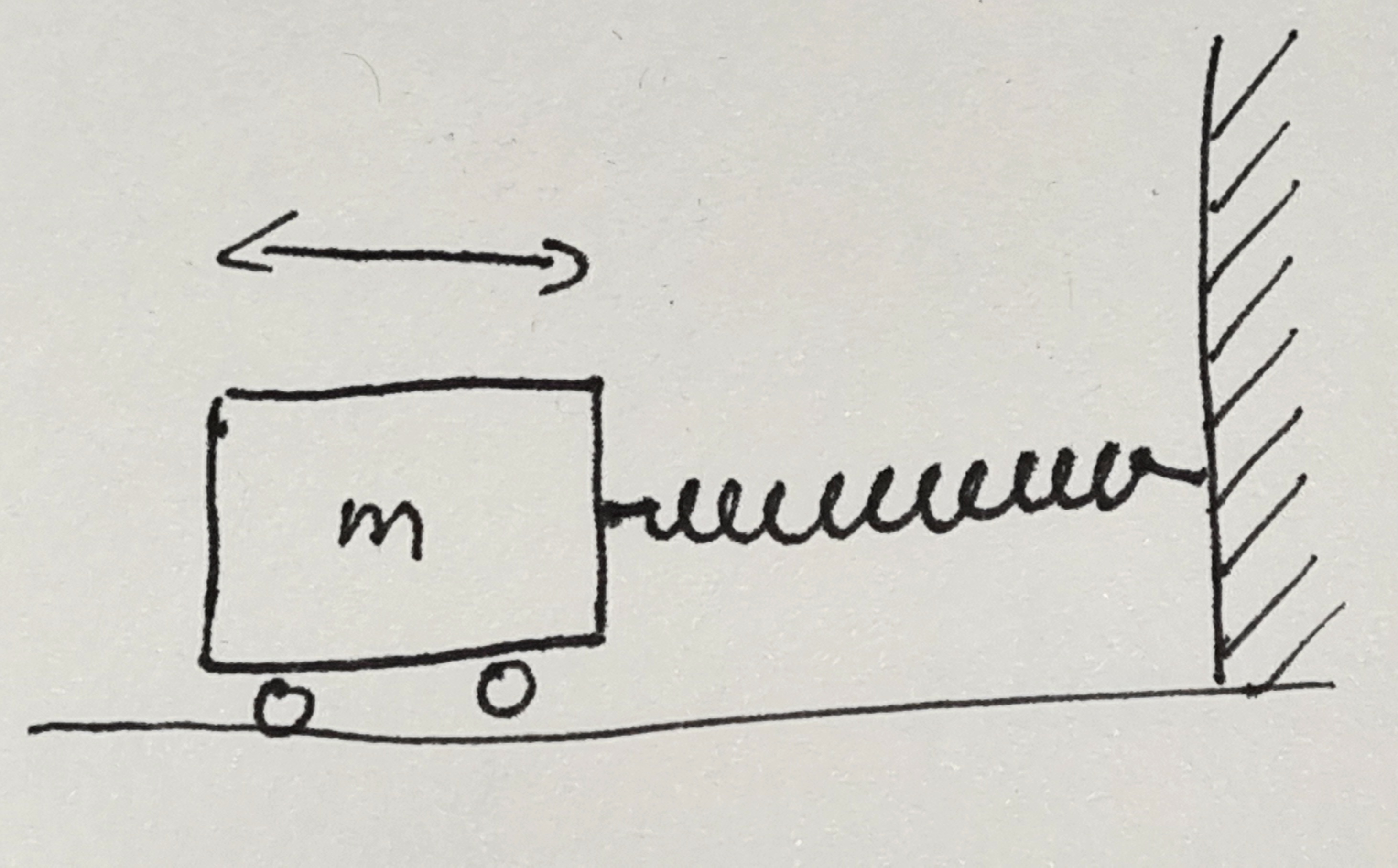
Let’s start with the most simple system that you will probably know from school. The mass on a spring is an idealized system consisting of a mass \(m\) attached to one end of a spring. The other end of the spring is held fixed. We imagine it being attached to a strong wall that will not move. The mass can only move in one direction and this motion will act to extend or contract the spring. The spring itself is assumed to be very light so that we can ignore its mass.
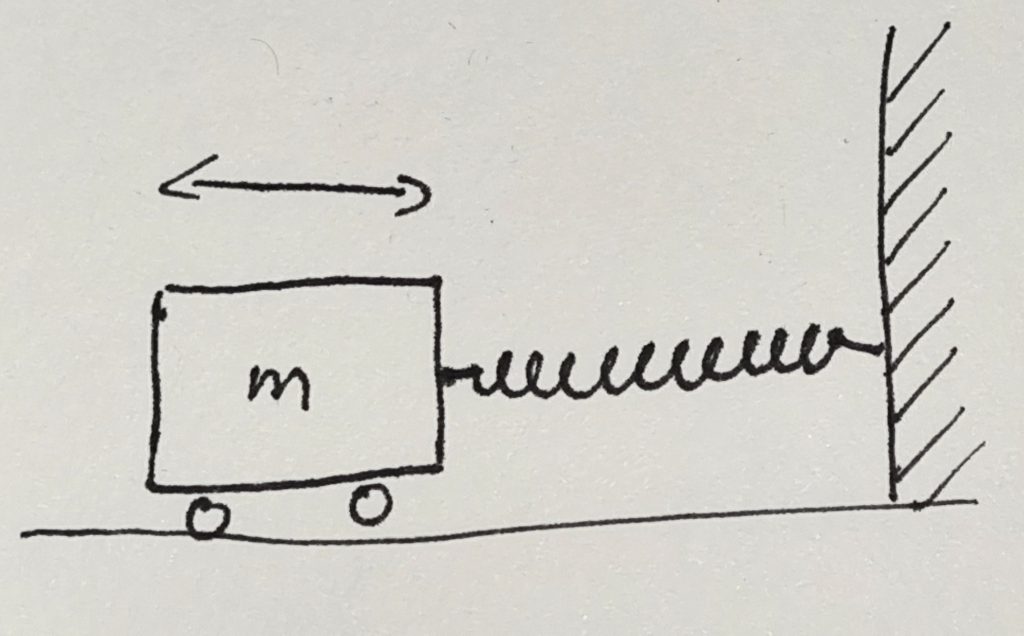
In the image, one end of the spring is attached to a wall and extends horizontally. The mass is attached to the other end and we assume that it can move without any friction. In the image, the mass has some wheels that allow it to move easily. We assume that the wheels do not create any resistance to the movement. I will come back to this assumption later.
When the system is in equilibrium, the mass will be at rest at some position along the horizontal axis. At this position, the spring does not exert any force on the mass and the mass will have no reason to move await from this equilibrium position. This is not very interesting, so let’s pull the mass away from its resting place. In what follows, I will measure the displacement, \(x\), of the mass from this equilibrium position. If we pull the mass to the right \(x\) will be positive. The spring will exert a force on the mass that will try to pull it back. The force will act towards the left, so we will assign it a negative value. A spring is designed so that the force is proportional to the displacement \(x\). The proportionality factor is called the spring constant \(k\). So we end up with a formula for the force, \[
F = -kx.
\] You can see that this formula also works if the mass is displaced to the left. In this case, \(x\) is negative and the force will be positive, pushing the mass to the right. Using the force, we can find out how the mass will move with time. The other equation that we will need for this is Newton’s law of motion, \(F = ma\) or \[
F = m \frac{d^2x}{dt^2}.
\] From these two equations we can eliminate the force and end up with \[
\frac{d^2x}{dt^2} = -\frac{k}{m}x.
\] This is a differential equation for the position \(x\). You can solve this by finding a function \(x(t)\) that, when differentiated twice, will give the same function but with a negative factor in front of it. From high school, you might remember that the \(\sin\) and \(\cos\) functions show this behavior, so let’s try it with \[
x(t) = x_0 \sin\left(\omega (t – t_0) \right).
\] Here \(x_0\), \(t_0\), and \(\omega\) are some constants that we don’t yet know. The idea is to try to keep the solution as general as possible and then see how we need to set these values to make it fit. So let’s try it out by inserting the function on both sides of our differential equation. \[
-\omega^2 x_0 \sin\left(\omega (t – t_0) \right) = -\frac{k}{m} x_0 \sin\left(\omega (t – t_0) \right).
\] Most terms in this equation cancel out and we are left with \[
\omega^2 = \frac{k}{m}.
\] This tells us that the equation of motion is satisfied whenever we choose \(\omega\) to satisfy this relation. Interestingly, the parameters \(x_0\) and \(t_0\) were canceled out which implies that we are free to choose any value for it. We could have also chosen \(\cos\) instead of \(\sin\) and ended up with the same result.
We now have a solution that depends on three parameters, \(x_0\), \(t_0\), and \(\omega\). We can do a dimensional analysis and see that \(x_0\) has units of length, \(t_0\) has units of time, and \(\omega\) is a frequency. Let’s take look at how these parameters change the behavior of the solution.
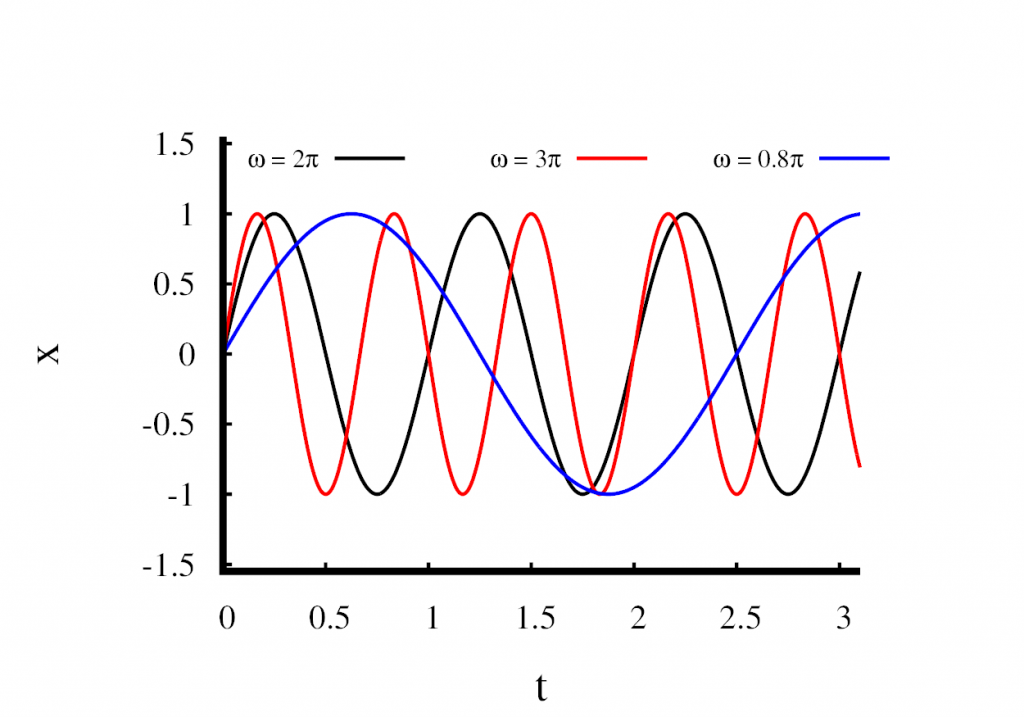
In the first figure, I have plotted three solutions in which I held \(x_0\) constant at 1m and \(t_0\) at zero. Only the parameter \(\omega\) is changed. You can see that \(\omega\) changes the speed at which the oscillations occur. A large value means that the oscillations are fast, and a small value means that the oscillations are slow. Looking at the \(\sin\) function, you can see that a full cycle finishes when the product \(\omega t\) reaches a value of \(2\pi\). This means that \(\omega\) is related to the frequency of the oscillation by \[
f = \frac{\omega}{2\pi}.
\] We call \(\omega\) the angular frequency.
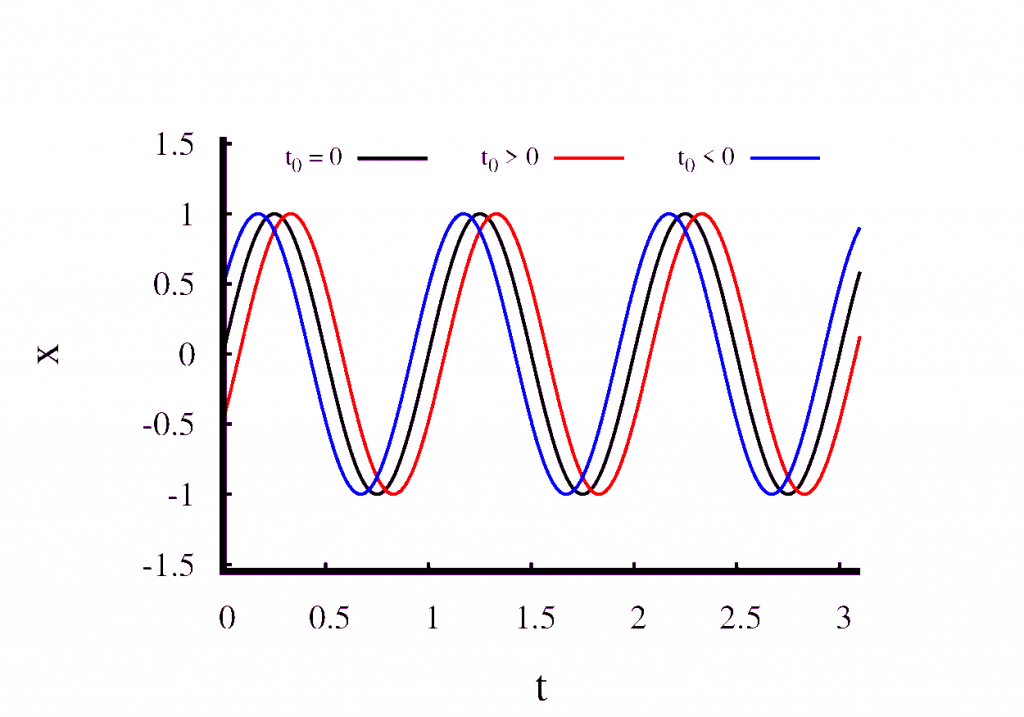
Next, have a look at what happens when we change \(t_0\) but keep all the other parameters fixed. This is shown in the second figure. You can see that \(t_0\) simply shifts the solution in time and does not modify it in any other way. We can choose \(t_0\) freely. All that this means is that we are at liberty to choose the point at which we start measuring time.
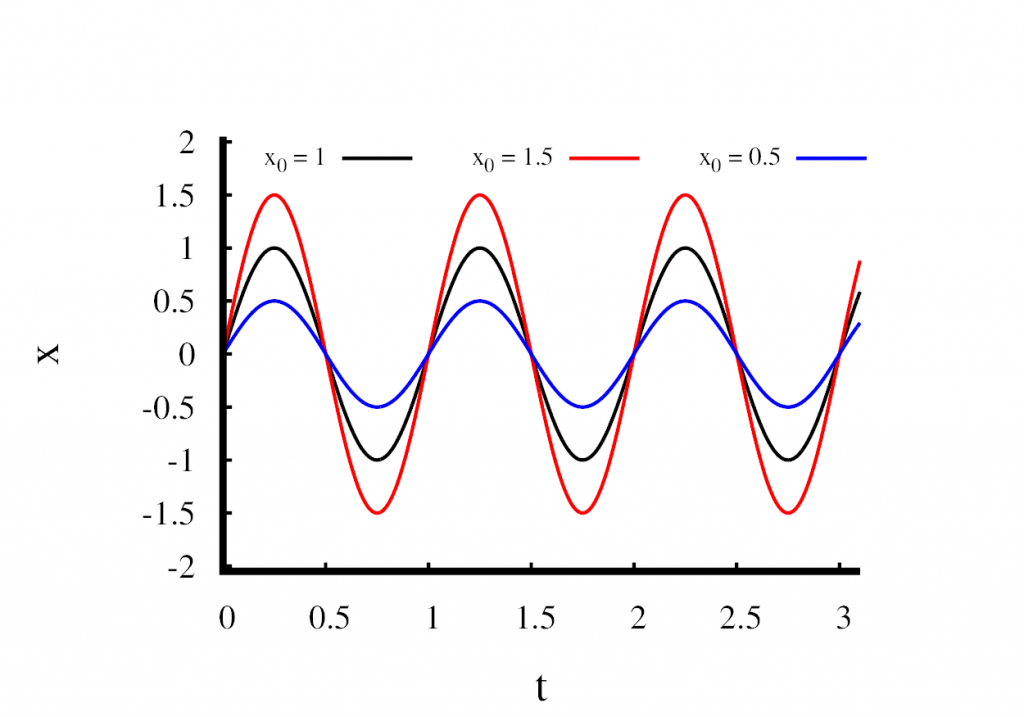
The third figure shows what happens when we modify \(x_0\) and keep all the other parameters fixed. You can clearly see that \(x_0\) changes the amplitude of the oscillation. Remember, that only the frequency \(\omega\) was fixed by the mass and the spring constant. We are free to choose \(x_0\) which means that the frequency is not influenced by our choice of \(x_0\). This leads to a very important conclusion about the harmonic oscillator.
The frequency of the oscillation is independent of its amplitude.
An energy perspective
In physics, it is often useful to look at the energy. In the spring mass system, we have two types of energy, the kinetic energy of the oscillating mass and the potential energy stored in the extended spring. We all remember the kinetic energy, \[
E_{\mathrm{kin}} = \frac{1}{2}m v^2.
\] To calculate the velocity, we have to take the derivative of the solution \(x(t)\), \[
v(t) = \omega x_0 \cos\left(\omega (t – t_0) \right).
\] The potential energy in the spring can be calculated by the work done as the spring is extended from the equilibrium length. You might remember the work to be force times distance. But in our system, the force changes with the distance. This means that the simple product has to be replaced with an integral, \[
E_{\mathrm{pot}} = \int_0^xkx\;dx = \frac{1}{2}kx^2.
\] We can take a look at the total energy over time. We know it should be constant, so let’s give it a try, \[
E_{\mathrm{tot}} = \frac{1}{2}m \omega^2 x_0^2\cos^2\left(\omega (t – t_0) \right) + \frac{1}{2}kx_0^2\sin^2\left(\omega (t – t_0) \right).
\] This can be simplified. First we can substitute \(\omega^2\) with \(k/m\). The terms in front of the trigonometric functions turn out to be the same and can be factorised, \[
E_{\mathrm{tot}} = \frac{1}{2}k x_0^2\left[\cos^2\left(\omega (t – t_0) \right) + \sin^2\left(\omega (t – t_0) \right)\right].
\] Next, Pythagoras tells us that \(\sin^2 + \cos^2 = 1\), so the bracket is just unity and we get \[
E_{\mathrm{tot}} = \frac{1}{2}k x_0^2.
\] This result confirms what we expected, the total energy is conserved and is equal to the maximum potential energy when the mass is at rest.
Another important thing to take away from this discussion is the relation between the potential energy \(E_{\mathrm{pot}} = \frac{1}{2}kx^2\) and the linear force \(F = -kx\). This relation more or less holds for any harmonic oscillator, not just the mass-and-spring system. Whenever we see a potential energy that is a parabolic function of the position, we can derive a linear force from it and we end up with a harmonic oscillator. This is why a potential of this form is also called a harmonic potential.
The oscillator in higher dimensions
The harmonic oscillator can easily be generalised to higher dimensions. Now, the displacement \(x\) is replaced by a vector \(\mathbf{r}\). The vector can be two-dimensional or three-dimensional. Then the force is also a vector and the force equation reads \[
\mathbf{F} = -k\mathbf{r}.
\] The equation states that the force always points from the position of the mass towards the origin. Just as with the one-dimensional case, the strength of the force is proportional to the distance from the origin. The force equation is relatively straightforward to grasp, but I find it slightly more instructive to look at the energy equation, \[
E_{\mathrm{pot}} = \frac{1}{2}k |\mathbf{r}|^2.
\] Let’s assume we are in three dimensions and the position vector is represented by its components \(\mathbf{r} = (x, y, z)\). We can use Pythagoras to calculate the magnitude of \(\mathbf{r}\) and end up with \[
E_{\mathrm{pot}} = \frac{1}{2}k \left(x^2 + y^2 + z^2\right).
\] Let’s write this a bit differently by expanding the bracket, \[
E_{\mathrm{pot}} = \frac{1}{2}k x^2 + \frac{1}{2}k y^2 + \frac{1}{2}k z^2.
\] You can see that this formula represents three independent harmonic oscillators. This is an important result. Imagine that the $y$ and $z$ coordinates were fixed to some value. Then the potential energy is that of a harmonic oscillator in x plus some constant offset. But it is always possible to add a constant to the potential energy because the physics only depends on potential differences. Equivalently, keeping $x$ and $z$ constant results in a harmonic oscillator in $y$.
Fifty Solitaires – It’s in the Cards
Posted 8th December 2021 by Holger Schmitz
This is the second instalment of my series in which I am developing a JavaScript solitaire game that allows the player to choose between many different rules of Solitaire. As I explained in my previous post, the motivation for this project came from an old bet that I made with a friend of mine. The goal was to develop a program that is able to play 50 types of solitaire games. In the last post, I discussed my plans for the application architecture and set up the React environment. Since then I have been made aware of the Storybook library that allows you to browse and test your react components during development. So I decided to make use of Storybook for this project. If you want to follow along you can find the code at Github.
In this post, I will set up Storybook and create the basic component to display a plain card. To initialise Storybook for my game, I opened up my terminal in the project folder and ran on the following command.
This installs all the tooling required for Storybook. It also creates some example files in the stories subfolder. I don’t need these examples and I also don’t like the way Storybook creates components in the same folder as the story definitions. So the first thing I did was to delete all the files in the src/stories/ folder.
My aim is to create playing cards and I was entertaining the thought of creating the appearance of the cards purely using Unicode characters and CSS. But then I came across a much more elegant solution. I found this SVG file on Wikimedia that is distributed under CC0 restrictions and therefore can be freely used for any purpose. The file contains images for all standard playing cards in an English deck. Looking at the source code of the SVG I discovered that each card was neatly organised as a single SVG group. This would allow me to manually add symbol tags around the group and make them directly available in react. I saved the file under src/assets/playing_cards.svg.
I like to put all my components in one place so in a new src\components subfolder I created the file Card.tsx. This is what the code for the component looks like.
import React from 'react';
import playingCards from '../assets/playing_cards.svg';
import './Card.css';
export enum CardSuit {
clubs = 'Clubs',
spades = 'Spades',
diamonds = 'Diamonds',
hearts = 'Hearts'
}
export enum CardValue {
ace='Ace',
two='Two',
three='Three',
four='Four',
five='Five',
six='Six',
seven='Seven',
eight='Eight',
nine='Nine',
ten='Ten',
jack='Jack',
queen='Queen',
king='King'
}
export interface CardProperties {
suit: CardSuit;
value: CardValue;
}
export function Card({suit, value}: CardProperties) {
return <svg className="card-component">
<use xlinkHref={`${playingCards}#${value.toLowerCase()}-${suit.toLowerCase()}`}></use>
</svg>
}You will notice that I have defined two enums, one for the suit and the other for the value of the card. The enums are strings to allow easy access to the symbols in the SVG file. I am not quite sure yet if I will be using these enums in other parts of the code. In that case, I should move them into a different module. But I will cross that bridge when I get there.
The Card component itself is relatively simple. It takes the suit and the card value as parameters and simply wraps an SVG element that links to a symbol in our playing_cards.svg file. The symbol name is constructed from the parameters passed into the component.
The next step was to create a simple story for the card component that allowed me to view it in Storybook. I created a file src/stories/Card.stories.tsx with the following content.
import React from 'react';
import { Card, CardProperties, CardSuit, CardValue } from '../components/Card';
export default {
component: Card,
title: 'Components/Card',
};
interface StoryCardProperties extends CardProperties {
style: { [key: string]: string}
}
function Template(args: StoryCardProperties) {
return <div style={args.style}><Card {...args} /></div>
};
export const Large = Template.bind({});
(Large as any).args = {
suit: CardSuit.spades,
value: CardValue.ace,
style: {
width: 380,
height: 560,
backgroundColor: '#008800',
padding: 10
}
};
export const Small = Template.bind({});
(Small as any).args = {
suit: CardSuit.spades,
value: CardValue.ace,
style: {
width: 200,
height: 290,
backgroundColor: '#008800',
padding: 10
}
};If you look closely, you will notice that the story is showing the card inside a div with a coloured background. I did this because the Card component doesn’t have an intrinsic size other than the SVG size. The container is needed to show that the card will adjust to different size layouts. I personally find it a bit annoying that I have to cast the stories Large and Small to any to be able to assign the args property. Maybe I’m doing something wrong here, or maybe the Storybook developers haven’t given enough attention to the TypeScript bindings. To start Storybook, I ran the command
The image below shows how the Card component looks inside Storybook.
The picture shows the way the card will look once I’m done. But I still have to edit playing_cards.svg so that the individual card symbols are defined correctly. Fortunately, I can edit the SVG and watch the effect of my changes directly in the browser through Storybook. I am not going to paste my edits here. This image shows an example of me editing the code.
The most important aspect of the edits is to get the viewBox right for each of the cards. You can also see the IDs of the symbols that need to match the card’s suit and value enums.
Conclusion
By creating a simple Card component, I have taken one big step in creating my solitaire game. Cards will be stacked to make the piles and I will have to create a way that the user can interact with the cards and the piles when playing the game. Right now the card is a passive component without any user interaction. My plan is to place all the code for the interactivity into a Pile component that will act as a container for one or more cards. But this will be the topic for my next post on this solitaire game.
Frege’s Numbers
Posted 19th November 2021 by Holger Schmitz
In a previous post, I started talking about natural numbers and how the Peano axioms define the relation between natural numbers. These axioms allow you to work with numbers and are good enough for most everyday uses. From a philosophical point of view, the Peano axioms have one big drawback. They only tell us how natural numbers behave but they don’t say anything about what natural numbers actually are. In the late 19th Century mathematicians started using set theory as the basis to define the axioms of arithmetic and other branches of mathematics. Two mathematicians, first Frege and later Bertrand Russell came up with a definition of natural numbers that gives us some insight into the nature of these elusive objects. In order to understand their definitions, I will first have to make the little excursion into set theory.
You may have encountered the basics of set theory already in primary school. Naïvely speaking sets are collections of things. Often the object in a set share some common property but this is not strictly necessary. You may have drawn Venn diagrams to depict sets, their unions and intersections. Something that is not taught in primary school is that you can define relations between sets that, in turn, define the so-called cardinality of a set.
Functions and Bijections
One of the central concepts is the mapping between two sets. For the following let’s assume we have two sets, \(\mathcal{A}\) and \(\mathcal{B}\). A function simply defines a rule that assigns an element of set \(\mathcal{B}\) to each element of set \(\mathcal{A}\). We call \(\mathcal{A}\) the domain of the function and \(\mathcal{B}\) the range of the function. If the function is named \(f\), then we write \[
f: \mathcal{A} \to \mathcal{B}
\] to indicate what the domain and the range of the function are.
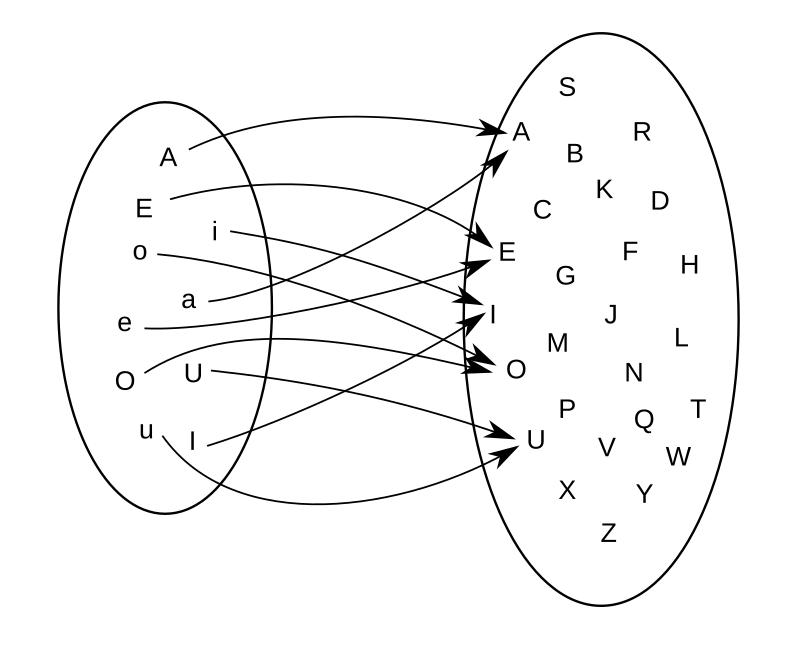
Example: For example, if \(\mathcal{A}\) is the set of uppercase and lowercase vowels, \[
\mathcal{A} = { A, E, I, O, U, a, e, i, o, u },
\] and \(\mathcal{B}\) is the set of all uppercase letters in the alphabet, \[
\mathcal{B} = { A, B, C, D, \ldots, Z}.
\]
Now we can define a function that assigns the uppercase letter in \(\mathcal{B}\) to each vowel in \(\mathcal{A}\). So the mapping looks like shown in the figure.
You will notice two properties about this function. Firstly, not all elements from \(\mathcal{B}\) appear as a mapping of an element from \(\mathcal{A}\). We say that the uppercase consonants in \(\mathcal{B}\) are not in the image of \(\mathcal{A}\).
The second thing to note is that some elements in \(\mathcal{B}\) appear twice. For example, both the lowercase e and the uppercase E in \(\mathcal{A}\) map to the same uppercase E in \(\mathcal{B}\).
Definition of a Bijection
The example shows a function that is not a bijection. In order to be a bijection, a function must ensure that each element in the range is mapped to by exactly one element from the range. In other words for a function \[
f: \mathcal{A} \to \mathcal{B}
\]
- every element in \(\mathcal{B}\) appears as a function value. No element is left out.
- no element in \(\mathcal{B}\) appears as a function value more than once.
A bijection implies a one-to-one relationship between the elements in set \(\mathcal{A}\) and set \(\mathcal{B}\).
Equinumerosity and Cardinality
Intuitively, it is clear that you can only have a bijection between two sets if they have the same number of elements. After all, each element in \(\mathcal{A}\) is mapped onto exactly one element in \(\mathcal{B}\). This can be used to define a relation between any two sets.
Two sets are called equinumerous if there exists a bijection between the two sets. Equinumerous literally means “having the same number”. But we have to be careful here because we don’t yet know what the term “number” is supposed to mean. That is the reason why we define the term by using bijections and not referring to any “amount” or “number of elements”. Instead of saying that two sets are equinumerous, we can also say that they have the same cardinality.
Now comes the clever bit that Frege proposed. Let’s create a class of sets that all share the same cardinality. We can do that because equinumerosity is an equivalence relation but I won’t go into detail about what that means. We will call this cardinality class \(N\), so \[
N(\mathcal{A})
\] is the class of all the sets that are equinumerous to \(\mathcal{A}\).
Intuitively we now have a class with all the sets that contain exactly one element, another class with all the sets that contain exactly two elements, and so forth. But we don’t know anything about numbers yet, so we also don’t really know what one and two are supposed to mean.
Constructing Natural Numbers
Now we have all the tools to construct the natural numbers \(\mathbb{N}\). Of course, we want our numbers to obey the Peano axioms, so we need two things. We need a zero element and we need a successor function \(S(n)\) that produces the next number from any given number.
The Zero Element
The zero-element is easily defined. We can construct the empty set, \[
\emptyset = \{\}.
\] This is the set with no elements in it. Now the zero-element is simply the cardinality class of the empty set, \[
0 = N(\emptyset).
\] This means that zero is a class of sets that all share the same cardinality as the empty set. You can show that this class consists of only one element, the empty set, by I won’t go into that here.
The Successor Function
Given that we have defined the zero element, \(0\), we can now define a set that contains zero as a single element, \[
\{0\}.
\] Intuitively, this set has one element and we can thus define the natural number \(1\) as the cardinality class of this set, \[
1 = N(\{0\}).
\] In general, given any natural number \(n\) we can define the successor \(S(n)\) by creating the cardinality class of the set that contains \(n\) together with all its predecessors, \[
n+1 = S(n) = N(\{0, 1, \ldots, n\}).
\] You might think that this definition is somewhat circular. We are defining the successor function by using the concept of the predecessors. But this is not as problematic as it might seem at first sight. We know that the predecessor of \(1\) is \(0\) and each time we construct the next natural number, we can keep track of all the predecessors that we have constructed so far.
Conclusion
The zero and the successor function defined above are enough to define all the natural numbers \(\mathbb{N}\). I will not go into the proof that all the Peano axioms are satisfied by this construction. It is relatively straightforward and not very instructive in my opinion. If you want, you can try doing the proof as an exercise.
I personally find the Frege definition of natural numbers the most satisfying. It tells us that a number is not just some random symbol that doesn’t relate to the real world. A natural number is the class of all sets that share the same property. Each set in the class has the same cardinality and we can identify the cardinality with that number. It means that any set of objects in the real world can be thought of as an instance of a number. The number itself is the collection of sets and the concrete set is contained within it as an element. For example, if you see five apples on a table, you can think of them as a manifestation of the number \(5\).
Another consequence of the definition of cardinality is that it gives us the ability to speak about infinities. A set might have an infinite number of elements. We already encountered \(\mathbb{N}\), the set of all natural numbers. Using the cardinality, we can compare infinite sets and create a hierarchy of infinities. I might talk about this more in a later post.
It would not be fair, however, if I didn’t mention some serious problems with the definition that I Frege came up with. The main problem arises because we are creating classes of sets without explicitly saying which elements we are allowing to be in those sets. This allows sets to contain arbitrary elements, including other sets. A set can even include itself as an element. This leads to the famous paradox by Russel which can be summarised as follows. Construct a set \(\mathcal{R}\) of all the sets that do not include themselves as an element. Then ask the question, does \(\mathcal{R}\) include itself? There are mathematical frameworks that attempt to save the essence of Frege’s definition of the natural numbers without running into these problems. In my personal opinion, they always lose some of the beauty and simplicity. But this is a necessary concession to make if you want to end up with a mathematical framework that doesn’t contain internal contradictions.
Computational Physics: Truncation and Rounding Errors
Posted 15th October 2021 by Holger Schmitz
In a previous post, I talked about accuracy and precision in numerical calculations. Ideally one would like to perform calculations that are perfect in these two aspects. However, this is almost never possible in practical situations. The reduction of accuracy or precision is due to two numerical errors. These errors can be classified into two main groups, round-off errors and truncation errors.
Rounding Error
Round-off errors occur due to the limits of numerical precision at which numbers are stored in the computer. As I discussed here a 32-bit floating-point number for example can only store up to 7 or 8 decimal digits. Not just the final result but every intermediate result of a calculation will be rounded to this precision. In some cases, this can result in a much lower precision of the final result. One instance where round-off errors can become a problem happens when the result of a calculation is given by the difference of two large numbers.
Truncation Error
Truncation errors occur because of approximations the numerical scheme makes with respect to the underlying model. The name truncation error stems from the fact that in most schemes the underlying model is first expressed as an infinite series which is then truncated allowing it to be calculated on a computer.
Example: Approximating Pi
Let’s start with a simple task. Use a series to approximate the value of \(\pi\).
Naive summation
One of the traditional ways of calculating \(\pi\) is by using the \(\arctan\) function together with the identity \[
\arctan(1) = \frac{\pi}{4}.
\] One can expand \(\arctan\) into its Taylor series, \[
\arctan(x)
= x – \frac{x^3}{3} +\frac{x^5}{5} – \frac{x^7}{7} + \ldots
= \sum_{n=0}^\infty \frac{(-1)^n x^{2n+1}}{2n+1}.
\] The terms of the series become increasingly smaller and you could try to add up all the terms up to some maximum \(N\) in the hope that the remaining infinite sum is small and can be neglected. Inserting \(x=1\) into the sum will give you an approximation for \(\pi\), \[
\pi \approx 4\sum_{n=0}^N \frac{(-1)^n }{2n+1}.
\]
Here are e implementations for this approximation in C++, Python and JavaScript.
C++
double pi_summation_slow(int N) {
double sum = 0.0;
int sign = 1;
for (int i=0; i<N; ++i) {
sum += sign/(2*i + 1.0);
sign = -sign;
}
return 4*sum;
}Python
def pi_summation_slow(N):
sum = 0.0
sign = 1
for i in range(0,N):
sum = sum + sign/(2*i + 1.0)
sign = -sign
return 4*sumJavaScript
function pi_summation_slow(N) {
let sum = 0.0;
let sign = 1;
for (let i=0; i<N; ++i) {
sum += sign/(2*i + 1.0);
sign = -sign;
}
return 4*sum;
}Let’s call this function with \(N=10\). All the results I am showing here are calculated using a Python implementation. We get a result of around 3.0418. The relative error is 0.0318 and is, of course, unacceptable. This error falls under the category of truncation errors because it is caused by not summing up enough terms of the Taylor series. Calling the function with \(N=1000\) gives us a result of 3.14059 with a relative error of \(3.183\times 10^{-4}\). The error has improved but is still far off from the possible \(10^{-14}\) to \(10^{-15}\) achievable in double-precision arithmetic. The figure below shows how the relative error decreases with the number of iterations.
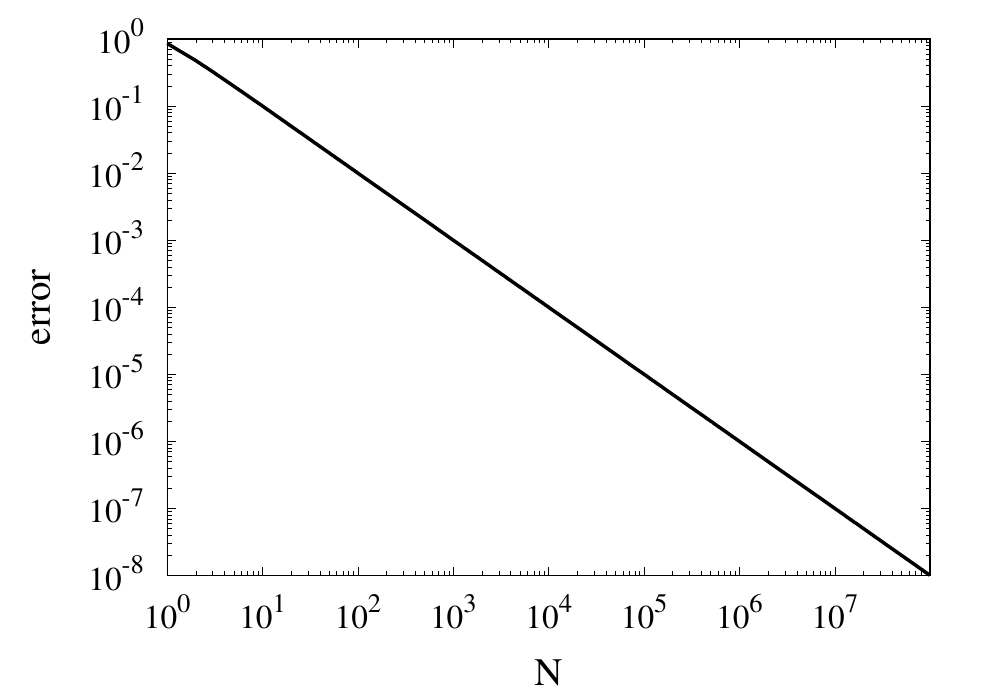
Relative error of the simple approximation of \( \pi \) depending on the number of iterations
From this curve, one h long m wl hat the error decreases with \(1/N\). If one extrapolates the curve, one finds that it would take \(10^{14}\) iterations to reach an error below \(10^{-14}\). Even if this was computationally feasible, the round-off errors of such a long sum would eventually prevent the error from being lowered to this limit.
Improvements using Machin’s formula
The technique of calculating \(\pi\) can be improved in two ways. Firstly, instead of using the Taylor series, you can use Euler’s series for the \(\arctan\) function.
\[
\arctan(x) = \sum_{n=0}^\infty \frac{2^{2n} (n!)^2}{(2n + 1)!} \frac{x^{2n + 1}}{(1 + x^2)^{n + 1}}.
\]
This series converges much more quickly than the Taylor series. The other way to improve convergence is to use trigonometric identities to come up with formulas that converge more quickly. One of the classic equations is the Machin formula for \(\pi\), first discovered by John Machin in 1706, \[
\frac{\pi}{4} = 4 \arctan \frac{1}{5} – \arctan \frac{1}{239}
\] Here are the implementations for this formula.
C++
double pi_summation_fast(int order) {
using boost::math::factorial;
double sum = 0.0;
for (unsigned int n=0; n<order; ++n) {
double f = factorial<double>(n);
double common = pow(2.0, 2*n)*f*f/factorial<double>(2*n + 1);
double A = pow(25./26., n+1)/pow(5., 2*n+1);
double B = pow(239.*239. / (239.*239. + 1.), n+1)/pow(239., 2*n+1);
sum += common*( 4*A - B );
}
return 4*sum;
}Python
def pi_summation_fast(N):
sum = 0.0
for n in range(0,N):
f = factorial(n)
common = math.pow(2.0, 2*n)*f*f/factorial(2*n + 1)
A = math.pow(25/26, n+1)/math.pow(5, 2*n+1)
B = math.pow(239*239 / (239*239 + 1), n+1)/math.pow(239, 2*n+1)
sum = sum + common*( 4*A - B )
return 4*sum;JavaScript
function pi_summation_fast(N) {
let sum = 0.0;
for (let n=0; n<N; ++n) {
const f = factorial(n);
const common = Math.pow(2.0, 2*n)*f*f/factorial(2*n + 1);
const A = pow(25/26, n+1)/pow(5, 2*n+1);
const B = pow(239*239 / (239*239 + 1), n+1)/pow(239, 2*n+1);
sum += common*( 4*A - B );
}
return 4*sum;
}The table below shows the computed values for \(\pi\) together with the relative error. You can see that each iteration reduces the error by more than an order of magnitude and only a few iterations are necessary to achieve machine precision accuracy.
| N | \(S_N\) | error |
|---|---|---|
| 1 | 3.060186968243409 | 0.02591223443732105 |
| 2 | 3.139082236428362 | 0.0007990906009289966 |
| 3 | 3.141509789149037 | 2.6376570705797483e-05 |
| 4 | 3.141589818359699 | 9.024817686074192e-07 |
| 5 | 3.141592554401089 | 3.157274505454055e-08 |
| 6 | 3.141592650066872 | 1.1213806035463463e-09 |
| 7 | 3.1415926534632903 | 4.0267094489200705e-11 |
| 8 | 3.1415926535852132 | 1.4578249079970333e-12 |
| 9 | 3.1415926535896266 | 5.3009244691058615e-14 |
| 10 | 3.1415926535897873 | 1.8376538159566985e-15 |
| 11 | 3.141592653589793 | 0.0 |
Example: Calculating sin(x)
Calculate the value of \(\sin(x)\) using it’s Taylor series around x=0.
The Taylor series for \(\sin(x)\) is \[
\sin x = \sum_{n=0}^\infty \frac{(-1)^n}{(2n+1)!}x^{2n+1}.
\] this series is much more well-behaved than the Taylor series for \(\arctan\) we saw above. Because of the factorial in the denominator, the individual terms of this series will converge reasonably quickly. Here are some naive implementations of this function where the infinite sum has been replaced by a sum from zero to \(N\).
C++
double taylor_sin(double x, int order)
{
using boost::math::factorial;
double sum = 0.0;
int sign = 1;
for (unsigned int n=0; n<order; ++n)
{
sum += sign*pow(x, 2*n + 1)/factorial<double>(2*n +1);
sign = -sign;
}
return sum;
}Python
def taylor_sin(x, N):
sum = 0.0
sign = 1
for n in range(0,N):
sum = sum + sign*math.pow(x, 2*n + 1)/factorial(2*n + 1)
sign = -sign
return sumJavaScript
function taylor_sin(x, N) {
let sum = 0.0;
let sign = 1;
for (let n=0; n<N; n++) {
sum += sign*pow(x, 2*n + 1)/factorial(2*n +1);
sign = -sign;
}
return sum;
}A good test for this function is the evaluation of \(\sin(x)\) at values \(x = k\pi\), where \(k\) is an integer. We know that \(\sin(k\pi) = 0\) and the return value from the numeric function can directly be used as the absolute error of the computation. The figure below shows results for some values of \(k\) plotted against \(N\).
For small values of \(k\), this series converges relatively quickly. But for larger \(k\) you can see that more and more terms are needed. The error even grows first before being reduced. Just like the example above, the truncation error requires large values of \(N\) to reach a good accuracy of the result. In practice, you would not calculate the \(\sin\) function this way. Instead you would make use of known properties, such as \(\sin(2k\pi + x) = \sin(x)\) for integer \(k\), to transform the argument into a range where fast convergence is guaranteed.
However, I would like to continue my analysis of this function because it shows two more interesting pitfalls when performing long sums. First, you will notice that the curves in the figure above show dashed lines for \(N>85\). This is because the implementation I showed above will actually fail with a range error. The pow function and the factorial both start producing numbers that exceed the valid range of double floating-point numbers. The quotient of the two, on the other hand, remains well-behaved. It is, therefore, better to write the Taylor series using a recursive definition of the terms.
\[
\sin x = \sum_{n=0}^\infty a_n(x),
\] with \[
a_0 = x
\] and \[
a_{n} = -\frac{x^2}{2n(2n+1)}a_{n-1}
\]
The implementations are given again below.
C++
double taylor_sin_opt(double x, int order)
{
double sum = x;
double an = x;
for (unsigned int n=1; n<order; ++n)
{
an = -x*x*an/(2*n*(2*n+1));
sum += an;
}
return sum;
}Python
def taylor_sin_opt(x, N):
sum = x
an = x
for n in range(1,N):
an = -x*x*an/(2*n*(2*n+1))
sum = sum + an
return sumJavaScript
function taylor_sin_opt(x, N) {
let sum = x;
let an = x;
for (let n=1; n<N; n++) {
an = -x*x*an/(2*n*(2*n+1));
sum += an;
}
return sum;
}The other takeaway from the graphs of the errors is that they don’t always converge to machine accuracy. The reason for this originates from fact that the initial terms of the sum can be quite large but with opposite signs. They should cancel each other out exactly, but they don’t because of numerical round-off errors.